Bayesian analysis of longitudinal traits in the Korea Association Resource (KARE) cohort

Study participants

The Korean Genome and Epidemiology Study (KoGES) was a large prospective cohort study that was initiated to solve public health issues and prepare for personalized and preventive health care in Korea [15]. The purpose of the KoGES was to build a genome epidemiological study platform for various researchers and examine the genetic and environmental etiology of complex traits and common diseases such as type 2 diabetes, hypertension, obesity, and metabolic syndrome in Korea. Data collection was initiated in 2001, and follow-up examinations for the participants have been conducted every 2 years. In particular, the availability of GWAS data and repeatedly measured traits in the KoGES Ansan-Ansung study facilitated the identification of genetic variants associated with various disease traits. The GWAS for the KoGES was known as the KARE cohort, which was launched to perform GWAS to discover the underlying genetic variants associated with diverse complex traits and diseases. The KARE data included 10,038 unrelated individuals aged 40–69 years, assembled through the KoGES Ansan-Ansung study, representing urban and countryside populations, respectively [16]. Our analyses utilized the KARE dataset from the baseline (2001–2002) to the sixth (2013–2014) follow-up.

Genotype data

The 10,038 participants in the KARE were genotyped at ~500,000 SNPs using the Affymetrix Genomewide Human SNP array 5.0. For SNP quality control (QC), we removed SNPs with minor allele frequency (MAF)<0.05, genotype calling rates <95%, and Hardy-Weinberg equilibrium p-values <10⁻⁶, resulting in 4,518,929 SNPs. For sample QC, we only preserved participants with consistent sex and calling rates >90%, resulting in 9,331 individuals. The SNP QC and sample QC were performed using PLINK (v1.90) [17]. We then imputed the genotyped SNP data using the Beagle 5.0 software [18] after the SNP and sample QCs. We restricted the analysis to Hapmap3 SNPs with MAF >0.05 and imputation R² >0.80, which consisted of 3,848,960 SNPs.

GWAS analysis

In the GWAS for cross-sectional obesity-related traits such as BMI, HIP, WST, and WHR, we performed linear mixed model (LMM) association analysis implemented in the BOLT-LMM (v2.3) software [19] using genotyped and imputed genetic variants from the KARE data [20]. The current analysis adjusted for age, age squared, sex, drinking, smoking status, and 10 genotype principal components (PCs). In order to obtain independent SNPs (i.e., a smaller number of clumps of correlated SNPs), we reduced the genome-wide scan using the PLINK clumping function based on empirical estimates of linkage disequilibrium (LD) between genetic variants loci (with four main flags: --clump-p1 5e-8 --clump-p2 1e-5 --clump-r2 0.1 --clump-kb 1000). The clumping procedure found index SNPs (p < 5 × 10⁻⁸) that were independent from each other and formed clumps of other SNPs that were located within 1,000 kb from each index SNP and in LD with the index SNP based on r² > 0.1. Clumps annotated to the same gene were further combined to the clump with the most significant index SNP.

Meta-analysis using trajectory model

To discover SNPs associated with the overall trend and trajectory of phenotypes, we prepared two different longitudinal outcomes (the average and trajectory), which were obtained from longitudinal BMI, HIP, WST, and WHR measurements (baseline to sixth follow-up). To assess the average outcome, we calculated the average BMI, HIP, WST, and WHR measurements over the six time points and then used the average values as the phenotype for GWAS analysis. To assess the trajectory outcome, we utilized the methodology in Gouveia et al. [13] designed to study cognitive trajectories. The LMM function implemented in the R package lme4 [21] was used to obtain the per-individual trajectory for all obesity-related traits. Specifically, we fitted the following mixed model for subject i at time j: yij=(β0+u0i)+(β1+u1i)x1ij+∑h=2qβhxhij+eij (i=1,…,n,j=1,…,6) where y_ij is a phenotypic value; u_0i is a random effect allowing variation around the intercept β₀;; u_1i is a random effect allowing variation around the slope for age covariate, β₁; x_hij (h = 1, …, q) are q covariates including age (h = 1) with fixed effects β_h; and e_ij is a random error. We assumed that the random intercept (u_0i) and the random slope (u_1i) were independent of each other and normally distributed. The models were adjusted for age squared, sex, drinking, and smoking status. We then used the predicted random slope (u_1i) from the model as the phenotype for a GWAS analysis of trajectory outcomes. All GWAS results for average and trajectory outcomes were obtained using BOLT-LMM software. In the GWAS for trajectory outcomes, the models were adjusted for only 10 genotype PCs to avoid over-adjustment.

Meta-analysis using a random-effects model

We utilized two different meta-analysis methods based on a fixed-effects model (Meta-Fixed) and a random-effects model (Meta-Random) to combine GWAS results for cross-sectional traits across all-time points (baseline to sixth follow-up). The Meta-Fixed method, as exemplified by the inverse-variance weighted method [22] and weighted sum-of-z-scores method [22], assumed that the magnitude of the true effects was common or fixed in every GWAS study and did not model heterogeneity. p-values for all GWAS analyses were converted to z-scores and then combined with different weights for each study according to their sample sizes. Meanwhile, the Meta-Random method proposed by DerSimonian and Laird [23] and Lee et al. [14] assumed that the true effect size of each study was sampled from an underlying distribution and modeled heterogeneity, explicitly. The Meta-Random method had two modifications: (1) accounting for correlation among test statistics based on the Lin and Sullivan method [24], and (2) focusing on heterogeneous effects conditioned on the Meta-Fixed method. The Meta-Random method can obtain higher power to detect heterogeneous effects than the Meta-Fixed method and it allows the testing of heterogeneous effect sizes between individual test statistics.

Grid-based Bayesian mixed model

To further discover SNPs associated with traits of interest and SNPs interacting with time/environmental factors, we considered the following Bayesian mixed model:

where y_i = (y_i1, …, y_ini)^T is an n_i × 1 phenotype vector of individual i; μ_i = μ1_ni is an n_i × 1 overall mean vector; xi=(xit,xig,xigg,xigt) is the design matrix corresponding to q time/environmental covariates, p SNPs, two-way interactions among p SNPs (resulting in total of p(p–1)/2 terms), and pq SNP-time/SNP-environment interactions; β = (β^tT, β^gT, β^ggT, β^gtT)^T is a vector of genetic effects, time/environmental effects, epistasis effects, and SNP-time/environment interactions; e_i is an n_i × 1 vector of random errors with e_i ~ N (0, σ²I_ni). For a given trait, we had n individuals, where individual i has phenotypic values measured at n_i time points (i = 1, …, n), and the total number of observations was N=∑i=1nni. To model the correlation among the repeated measurements of the same individual, we partitioned the observed time interval by k pre-specified grid points, t = (t₁, …, t_k)^T, and defined ν_i as a k × 1 vector of random effects at the grid time points with ν_i ~ N(0, D), where D is a k × k covariance matrix. We also defined the incidence matrix p_i as pi=(pi1T,…,piniT)T. If all subjects had k observations measured exactly on the k grid time points, then p_i became an identity matrix. We applied a linear interpolation procedure to any observation that did not fall on any one of k grid time points. When the jth measurement of individual i fell at time t, which was in between the grid points t_r and t_r+1 (t_r ≤ t ≤ t_r+1), we set pij=(0(r-1)T,tr+1-ttr+1-tr,t-trtr+1-tr,0(k-r-1)T). When t = t_r, we get pij=(0(r-1)T,1,0(k-r)T).

For Bayesian estimation of the mixed-effects model (1), we applied the modified Cholesky decomposition of Chen and Dunson [25] to the k × k covariance matrix D, resulting in the decomposition, D = ΔΨΨ^TΔ, where Δ is a nonnegative k × k diagonal matrix and Ψ is a k × k lower triangular with 1’s in the diagonal elements. We re-parameterized model (1) as

where b_i = (b_i1, … b_ik)^T such that b_ij ~ N(0,1) and bij⊥bij′ (j≠j′), j = 1, …, k.

As priors for Δ and Ψ, we defined two vectors δ = (δ_l : l = 1, …, k)^T and ψ = (ψ_ml : m = 2, …, k; l = 1, …, m − 1)^T. The prior distribution for δ is P(δ)=∏l=1kP(δl)=∏l=1kN+(δl∣ml0,sl02) where N+(δl∣ml0,sl02) was the density of a half normal distribution that was a N(δl∣ml0,sl02) density truncated below by zero. The prior distribution for ψ was P(ψ)=dN(ψ0,R0) where ψ₀ and R₀ are pre-specified hyperparameters. The joint prior distribution of b=(b1T,…,bnT)T was P(b)=dN(0,Ink). The prior for the ath genetic effect was a normal distribution, P(βa∣γa,σβ2)=dN(0,γaσβ2) and the prior for the variance σβ2 was a scaled inverse χ² distribution. The prior for the overall mean μ was given by P(ψ)=dN(η0,τ02). The prior for the residual variance σ² was chosen as a scaled inverse χ² distribution, P(σ2)=dinv-χ2(νσ,sσ2). The joint posterior distribution was proportional to the product of the likelihood and the prior distributions of all unknown parameters. We utilized Metropolis-Hastings and Gibbs sampling algorithms, and alternately updated each unknown parameter or set of unknown parameters conditional on all the other parameters and the observed data.

The posterior samples can be used to approximate the posterior distribution of the parameters. The posterior inclusion probability of each SNP was calculated using its inclusion proportion in the Markov chain Monte Carlo samples. The Bayes factor (BF) can be calculated to quantify the evidence for the inclusion of a specific SNP against the exclusion of that SNP. Jeffreys [26] and Yandell et al. [27] suggested the following criteria for judging the significance of each SNP: weak support if the BF falls between 3 and 10; moderate support if the BF falls between 10 and 30; and strong support if the BF is larger than 30 (i.e., log₂(BF) > 6.8). A critical issue with the proposed Bayesian model was how to choose an optimal number of grid points, k. We achieved the goal by evaluating the goodness of the predictive distributions of our Bayesian models. Spiegelhalter et al. [11] proposed the DIC and Ando [12] developed the BPIC. We select the optimal number of grid points for our model by minimizing the DIC or simplified BPIC scores. The proposed methods were implemented in an R package named Gridbayes [10], which is available for download at https://github.com/wonilchung/GridBayes.

GWAS analysis

We conducted a GWAS analysis of KARE data on longitudinal obesity-related phenotypes such as BMI, HIP, WST, and WHR. Seven covariates (age, age squared, sex, area, drinking, smoking status and 10 genotype PCs) were included in the analysis. Among 9,331 individuals, we selected 4,621 individuals who had no missing values for either phenotypes or covariates. The number of measurements for each individual was six, and thus the total number of observations was 27,726. Hapmap3 SNPs with MAF > 0.05 and imputation R² > 0.8 were retained for the GWAS analyses, resulting in 3,848,960 SNPs.

GWAS analyses for cross-sectional obesity-related phenotypes were performed using LMM association analysis implemented in the BOLT-LMM. To assess the cross-sectional outcomes, we analyzed all measurements (baseline to sixth follow-up) separately for each phenotype. Fig. 1 displays Manhattan plots for the baseline BMI, HIP, WST, and WHR measurements and Supplementary Figs. 1–5 in the supplementary materials show the Manhattan plots for the second, third, fourth, fifth, and sixth measurements. Supplementary Figs. 6–11 show the corresponding Quantile-Quantile (Q-Q) plots. For BMI, one SNP on chromosome 6 (baseline) reached GWAS significance (p < 5 × 10⁻⁸), and for HIP, five SNPs on chromosome 11 (baseline), one SNP on chromosome 12 (third follow-up), two SNPs on chromosome 12 (fourth follow-up), and one SNP on chromosome 6 (sixth follow-up) exceeded the threshold for GWAS significance in Supplementary Table 1. For WST, 11 SNPs on chromosome 11 (baseline) and for WHR, 16 SNPs on chromosome 12 (second follow-up), one SNP on chromosome 12 (fifth follow-up), one SNP on chromosome 18 (second follow-up), and one SNP on chromosome 18 (fifth follow-up) reached GWAS significance (see Supplementary Table 1).

Fig. 1

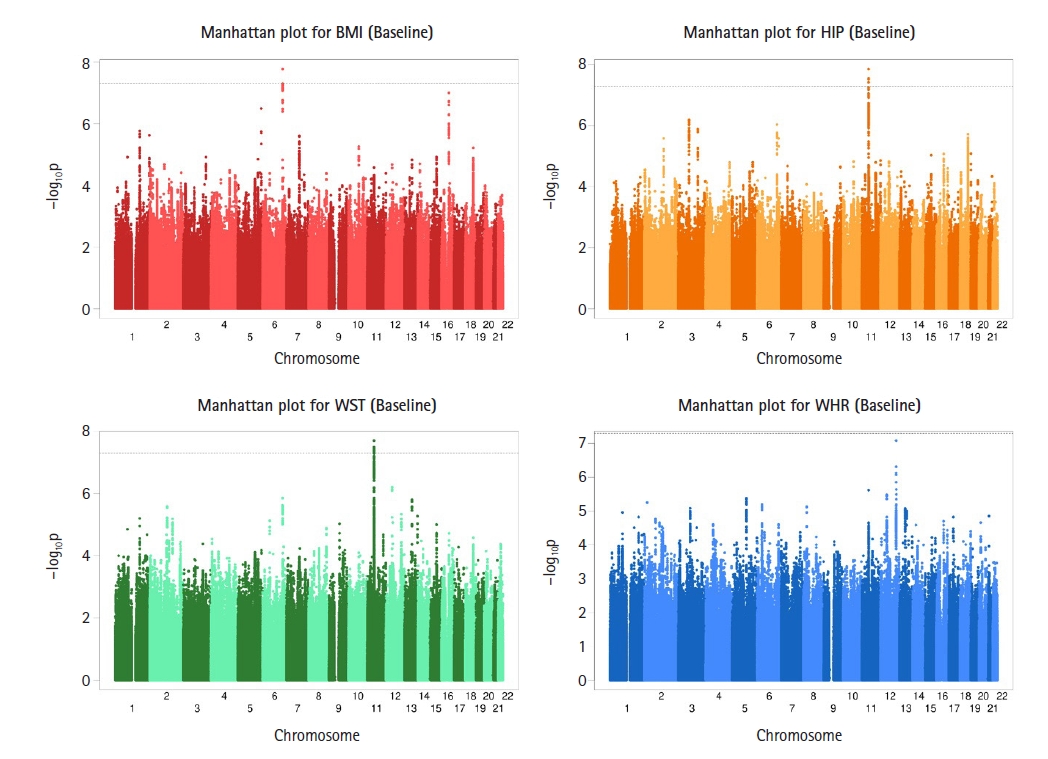
Genome-wide Manhattan plots of −log₁₀(p-value) for association with baseline body mass index (BMI), hip circumference (HIP), waist circumference (WST), and waist-hip ratio (WHR) measurements using BOLT-LMM. For BMI, one single nucleotide polymorphism (SNP) on chromosome 6 reached genome-wide association studies (GWAS) significance, for HIP, five SNPs on chromosome 11 exceeded the threshold for GWAS significance and for WST, eleven SNPs on chromosome 11 reached GWAS significance.

Meta-analysis

In order to identify SNPs associated with the overall trend and trajectory of the phenotype, we utilized two types of longitudinal outcomes (average and trajectory), obtained for BMI, HIP, WST, and WHR measurements across consecutive examinations of each individual. For the average outcomes, we calculated the average of all measurements from baseline to sixth follow-up. For the trajectory outcomes, we estimated the per-individual trajectory for all obesity-related traits by fitting a mixed model in the R package lme4 [21]. The model contained a random intercept and a slope for age, as well as other covariates such as age squared, sex, area, and drinking and smoking status. The predicted random slopes of all individuals for age were used as the phenotype for GWAS on trajectory outcomes. We performed BOLT-LMM analyses with these average and trajectory outcomes for four obesity-related traits. Supplementary Fig. 12 shows Manhattan plots for the average outcomes, and Supplementary Fig. 13 shows Manhattan plots for the trajectory outcomes. Supplementary Figs. 14 and 15 show the corresponding Q-Q plots. No GWAS significant SNPs were found for either the average or trajectory outcomes, suggesting that a simple average and simple trajectory of longitudinal outcomes cannot effectively combine the cross-sectional traits; therefore, more sophisticated approaches are necessary.

To effectively combine all GWAS results for cross-sectional traits, we performed two different meta-analyses (Meta-Fixed and Meta-Random; see the Methods section) using RE2C software [14]. Because the Meta-Random method accounted for correlation among test statistics for all cross-sectional traits, it would be more appropriate than Meta-Fixed method for our analysis. Supplementary Fig. 16 shows Manhattan plots for the Meta-Fixed method, and Fig. 2 shows Manhattan plots for the Meta-Random method. Supplementary Figs. 17 and 18 show the corresponding Q-Q plots. From the results of Meta-Fixed method, for BMI, two SNPs on chromosome 5 and seven SNPs on chromosome 16 reached GWAS significance, and for WHR, five SNPs on chromosome 12 reached GWAS significance (Supplementary Table 2). From the results of the Meta-Random method, for BMI, two SNPs on chromosome 5 and seven SNPs on chromosome 16 reached GWAS significance, and for WHR, six SNPs on chromosome 12 reached GWAS significance (Supplementary Table 3). Supplementary Fig. 19 shows the scatter plots of −log₁₀(p-value) in GWAS for four longitudinal traits between the Meta-Random method and Meta-Fixed method. As expected, the p-values with the Meta-Random method were smaller than those obtained with the Meta-Fixed method, but there was reasonable concordance between them. In Fig. 3, it can be seen that p-values of the Meta-Random method were more significant than those of the baseline analysis in general.

Fig. 2

Genome-wide Manhattan plots of −log₁₀(p-value) for associations with longitudinal body mass index (BMI), hip circumference (HIP), waist circumference (WST), and waist-hip ratio (WHR) measurements using the Meta-Random method. Two single nucleotide polymorphisms (SNPs) on chromosome 5 and seven SNPs on chromosome 16 reached genome-wide association studies (GWAS) significance and for WHR, six SNPs on chromosome 12 reached GWAS significance.

Fig. 3

Scatter plots of −log₁₀(p-value) for association for longitudinal body mass index (BMI), hip circumference (HIP), waist circumference (WST), and waist-hip ratio (WHR) measurements between the Meta-Random method and baseline analysis. The p-values of the Meta-Random method were more significant than those of the baseline analysis in general.

Bayesian analysis

For our Bayesian analysis, a subset of SNPs was selected using LD clumping analysis based on the results of the Meta-Random method to only include SNPs that are not highly correlated with each other (with correlation < 0.5 to avoid multicollinearity). For our Bayesian analysis, we picked a list of the 4,124 SNPs from the LD clumping analyses (option: --clump -kb 250 −p1 0.001 −p2 0.01 −r2 0.5) using PLINK (v1.90) based on summary statistics from the Meta-Random analysis for the four obesity-related traits. Again, our Bayesian analysis included age, age squared, sex, area, drinking, smoking status, and 10 genotype PCs as covariates. The number of grid time points was set to 3 for the analysis based on the DIC and simplified BPIC scores with a different number of grid points (results not shown). Fig. 4 shows the one-dimensional genome-wide profiles of 2log(BF) for the combined effects (main, epistasis, and SNP-age interactions). Based on the criteria suggested in Jeffreys [26] and Yandell et al. [27], we found 112 SNPs with strong signals (i.e., log₂(BF) > 6.8) for BMI, 20 SNPs for HIP, 10 SNPs for WST, and 6 SNPs for WHR in Supplementary Table 4. We compared the results of our Bayesian analysis with p-values from the baseline, average, trajectory, and Meta-Random methods and discovered various newly detected novel loci and reasonable concordance among different approaches.

Fig. 4

Genome-wide profiles of 2log(BF) for all combined effects with body mass index (BMI), hip circumference (HIP), waist circumference (WST), and waist-hip ratio (WHR) measurements from Gridbayes. The two dashed horizontal lines represent the genome-wide thresholds for moderate (Bayes factor [BF]=10) strong (BF=30) genome-wide associations. We found 112 single nucleotide polymorphisms (SNPs) with strong signals for BMI, 20 SNPs for HIP, 10 SNPs for WST, and six SNPs for WHR.

Also, our Bayesian method can discover SNPs interacting with environmental covariates including age, we needed to investigate whether the identified SNPs interacted with age covariate. For SNP-age interaction, we fitted the LMM with each of the four traits (BMI, HIP, WST, and WHR) as a response variable and eight covariates (SNP, age, age squared, sex, area, drinking and smoking status, SNP-age interaction) as predictors: yij=(β0+u0i)+∑h=17βhxhij+eij (i=1,…,n,j=1,…,6) where y_ij is a phenotypic value, u_0i is a random effect allowing variation around the intercept β₀, β_h denotes genetic and nongenetic effects for eight covariate values x_hij (including SNP-age interaction), and e_ij is a random error. Based on p-values for SNP-age interaction in the LMM, we found 30 significant SNPs interacting with age for BMI, three SNPs for HIP, three SNPs for WST, and one SNP for WHR in Table 1, meaning that almost 25% of the identified SNPs using Gridbayes had significant p-values for SNP-age interaction. Based on the results of SNP-age interaction, as shown in Table 1, we displayed age-specific changes in BMI for three different genotypes (0, 1, and 2) at four SNPs (Chr5:149489242, Chr6:96377858, Chr10:18571215, and Chr20:40534573), age-specific changes in HIP at one SNP (Chr8:98187086) and age-specific changes in WST at one SNP (Chr2:133806432) in Fig. 5. These figures clearly showed different slopes in phenotypic values over six time points for three genotypes, meaning that there were SNP-age interactions at the identified genetic loci by Gridbayes.

Table 1

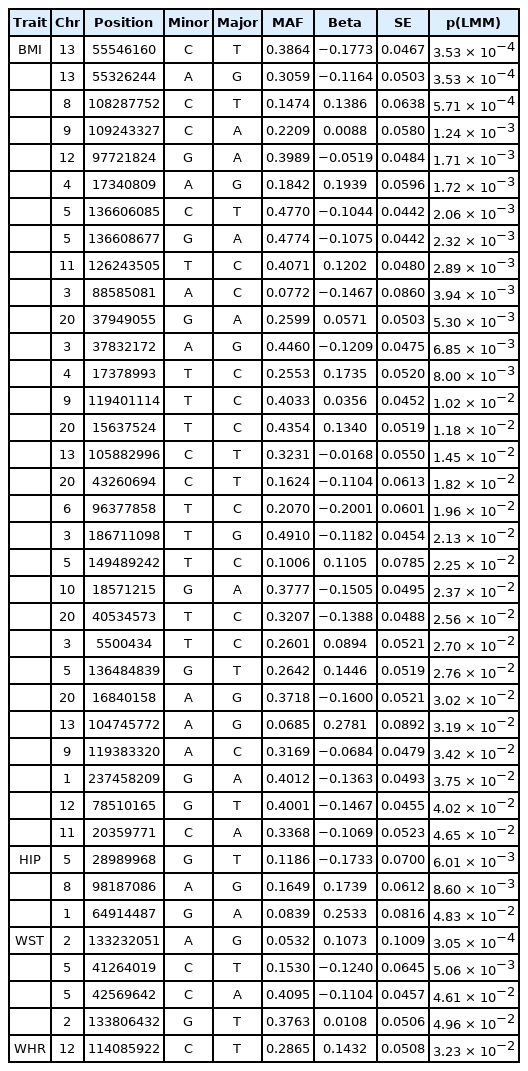
Genome-wide association results for BMI, HIP, WST, and WHR-associated SNPs with a p-value < 0.05 using the LMM method

Fig. 5

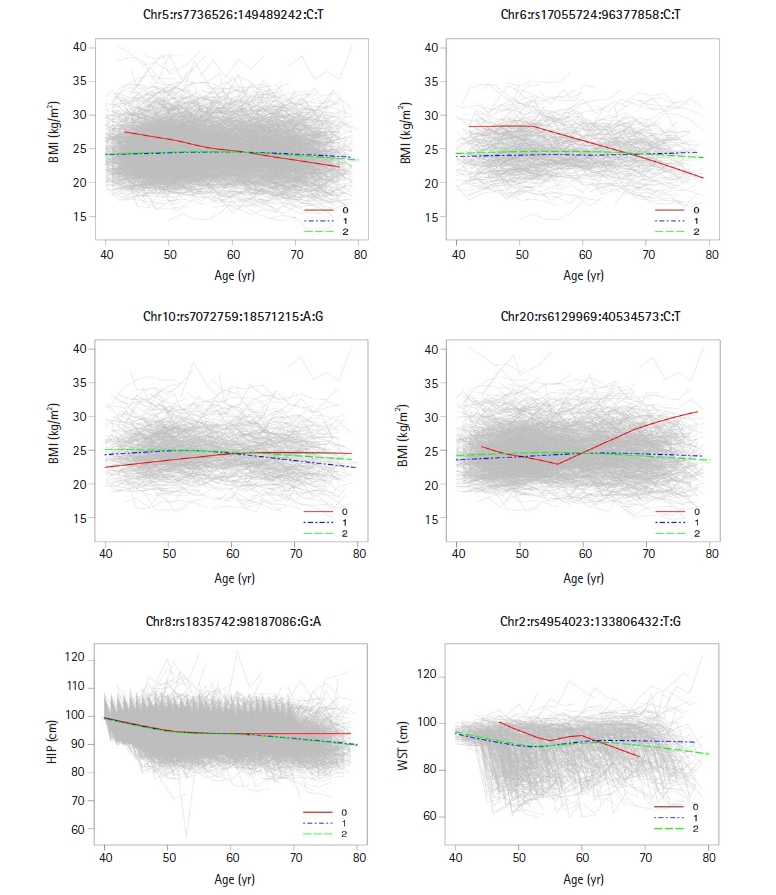
Time-specific changes in body mass index (BMI) for three different genotypes (0, 1, and 2) at four single nucleotide polymorphisms (SNPs) (Chr5:149489242, Chr6:96377858, Chr10:18571215, and Chr20:40534573), age-specific changes in hip circumference (HIP) at one SNP (Chr8:98187086), and age-specific changes in waist circumference (WST) at one SNP (Chr2:133806432). The figures clearly show different slopes in phenotypic values over six time points for three genotypes, meaning that there are SNP-age interactions at identified the genetic loci.