 |
 |
- Search
| Genomics Inform > Volume 20(2); 2022 > Article |
|
Abstract
A survival prediction model has recently been developed to evaluate the prognosis of resected nonmetastatic pancreatic ductal adenocarcinoma based on a Cox model using two nationwide databases: Surveillance, Epidemiology and End Results (SEER) and Korea Tumor Registry System-Biliary Pancreas (KOTUS-BP). In this study, we applied two machine learning methodsŌĆörandom survival forests (RSF) and support vector machines (SVM)ŌĆöfor survival analysis and compared their prediction performance using the SEER and KOTUS-BP datasets. Three schemes were used for model development and evaluation. First, we utilized data from SEER for model development and used data from KOTUS-BP for external evaluation. Second, these two datasets were swapped by taking data from KOTUS-BP for model development and data from SEER for external evaluation. Finally, we mixed these two datasets half and half and utilized the mixed datasets for model development and validation. We used 9,624 patients from SEER and 3,281 patients from KOTUS-BP to construct a prediction model with seven covariates: age, sex, histologic differentiation, adjuvant treatment, resection margin status, and the American Joint Committee on Cancer 8th edition T-stage and N-stage. Comparing the three schemes, the performance of the Cox model, RSF, and SVM was better when using the mixed datasets than when using the unmixed datasets. When using the mixed datasets, the C-index, 1-year, 2-year, and 3-year time-dependent areas under the curve for the Cox model were 0.644, 0.698, 0.680, and 0.687, respectively. The Cox model performed slightly better than RSF and SVM.
Pancreatic cancer is well-known as one of the most lethal cancers worldwide because it has a 5-year overall survival rate of 12.6% as of 2020, while other cancers have 5-year overall survival rates of over 80%. The survival rate strongly depends on the stage of cancer and disease severity. For example, in patients with stage I pancreatic cancer, the 5-year postoperative survival rate is 70.32%, while in patients with stage IV cancer, the 5-year postoperative survival rate is only 3.52%. Therefore, early diagnosis and prediction have been considered promising ways to improve the survival rate of pancreatic cancer.
A survival prediction model for resected pancreatic ductal adenocarcinoma (PDAC) was recently developed with data from the Surveillance, Epidemiology and End Results (SEER) database from the United States and external validation using the nationwide Korea Tumor Registry System-Biliary Pancreas (KOTUS-BP) dataset [1]. This prediction model uses a Cox model, which assumes linear associations with many clinicopathologic features. However, it is necessary to investigate nonlinear relationships or complex interactions between clinicopathologic features associated with the survival time. To this end, we applied two machine learning (ML) methodsŌĆörandom survival forests (RSF) and support vector machines (SVM)ŌĆöto construct predictive models for survival analysis.
In this study, three different schemes were conducted for model development and external evaluation. First, we utilized data from SEER for model development and data from KOTUS-BP for external evaluation. Secondly, these two datasets were used in reverse by taking data from KOTUS-BP for model development and data from SEER for external evaluation. Finally, we mixed these two datasets half and half and utilized the mixed datasets for model development and external validation.
For each of the three different schemes, we developed prediction models using a Cox proportional hazards model, RSF, and SVM. We compared their performance in terms of the C-index and 1-year, 2-year, and 3-year time-dependent areas under the curve (AUCs).
This study utilized two nationwide databases: the SEER database from the United States and the KOTUS-BP database from Korea. The datasets were pre-processed as described elsewhere [1]. In the screening process, 9,624 patients from SEER and 3,281 patients from KOTUS-BP were selected. Due to the different sets of covariates in the two datasets, only seven covariatesŌĆöincluding age, sex, histologic differentiation, adjuvant treatment, resection margin status, and the American Joint Committee on Cancer (AJCC) 8th edition T-stage and N-stageŌĆöwere utilized in this study.
The SEER database, which has been maintained by the National Cancer Institute in the United States since 1975, is one of the largest and highest-quality cohort studies, whereas the KOTUS-BP database was launched by the Korean Association of Hepato-Biliary-Pancreatic Surgery in 2014 and has been prospectively registered and regularly managed by pancreatobiliary surgeons at specialized centers in Korea. To unify the study period, patients who underwent upfront curative-intent pancreatectomy between 2004 and 2016 were included.
Three schemes for model development and external validation were conducted. First, we utilized data from SEER for model development and data from KOTUS-BP for validation. Second, we swapped the roles of these two datasets for model development and evaluation. Finally, we mixed these two datasets half and half, and utilized the mixed datasets for model development and external validation.
The Cox proportional hazard (Cox-PH) model and the two ML models had different schemes for the model development process, as shown in Fig. 1, although we used all seven covariates in the Cox-PH model and both ML survival models. While the Cox-PH model was constructed without considering any hyperparameters, both RSF and SVM models require cross-validation (CV) to select the set of hyperparameters that build the best model. First, the model development dataset was divided into 10 subsets. For 10-fold CV, nine of the 10 subsets were used for the training set and the other subset was used for the validation set. The average Harrell C-index of the validation sets in a total of 10 iterations was calculated to compare the performance of models. The final model was then constructed with the entire model development dataset and the set of hyperparameters that resulted in the best average Harrell C-index during 10-fold CV.
In prospective cohort studies, survival analysis has been useful to investigate the prognostic factors associated with the survival time and to predict disease processes. In traditional survival analysis, a survival prediction model has been constructed on the basis of demographic and clinicopathologic information. In recent years, there has been considerable interest in applying ML methods to predict the survival of cancer patients using a considerable amount of genomic information including traditional clinical covariates. An advantage of ML methods over the classical Cox regression models is their ability to model complicated associations between the survival time and risk factors, leading to better prediction. Unlike regression and classification settings, standard ML methods cannot be directly applied to censored survival data. With consideration of the censoring mechanism, several ML methods have been extended to survival data, such as bagging survival trees [2], RSF [3,4], SVM for survival analysis [5-8], and CoxBoosting [9]. Among these methods, RSF and SVM for survival analysis were used to develop prediction models for PDAC patients in this study.
The RSF method is an extension of BreimanŌĆÖs random forest method to right-censored survival data by using a forest of survival trees for prediction. Similar to regression and classification settings, RSF is an ensemble learner formed by averaging a tree base-learner. In survival settings, a binary survival tree is the base-learner, and the ensemble learner is formed by averaging each treeŌĆÖs Nelson-AalenŌĆÖs cumulative hazard function.
There are four main steps in RSF: (1) Draw B bootstrap samples randomly from the given dataset. Since one-third of the training set data is not present in the bootstrapping sample, this leftover data is known as the out-of-bag (OOB) data. (2) For each sample, construct a survival tree using a randomly selected subset of variables among all available variables, and split the nodes using the candidate variables that maximize the survival difference between child nodes. Here, the survival difference is measured by three criteria: the log-rank statistic, gradient-based Breier score, and log-rank score. (3) Grow the tree to the full size with the constraint that a terminal node should contain a certain number of unique uncensored patients. (4) For each terminal node, calculate the cumulative hazard function (CHF) based on the Nelson-Aalen estimator and take the ensemble CHF of the OOB data by averaging the CHF of each tree.
The SVM method of supervised learning has been very successful, mostly in classification and then extended to the regression problem. The main idea of SVM is to minimize the ╬Ą-insensitive loss function, max(0,|f(xi)-yi |-╬Ą), with a regularization parameter. Here, f(xi), yi, and ╬Ą are the predicted value, the actual value, and the acceptable margin of error, respectively.
To take into account censored survival data, SVM for regression on the censored data (SVCR) has been proposed by imposing constraints on the SVM formulation for two comparable cases [5,6]. In other words, for censored data, the time to event after censoring is unknown and thus predictions greater than the censoring time are not required to be penalized. However, all survival predictions less than the censoring time are penalized, while uncensored data are treated in the same way as in the ordinary regression approach, since the exact event time is known. A prior study compared three types of SVM [8], including a regression approach, a ranking approach and a hybrid approach combining the regression and ranking approaches. All types of SVM share a common frame, but they differ in their objective function and constraints. In this paper, two types of SVM were considered: the SVCR model proposed by Shivaswamy et al. [5] and ranking support vector machines (RankSVMs) proposed by Van Belle et al. [8]. These two models have been summarized in detail and compared elsewhere [7].
In the SVM model, overall survival time, y, is explained by the clinical variables x as y=Žå(x)+ŽĄ, where Žå(ŌłÖ) is called the feature map. Since the feature map usually implies a higher-dimensional space, it is unusual to calculate the feature map itself. Instead, the feature map is directly calculated by kernel k(xi, xj)=Žå(xi)T Žå(xj) for variable x between patients i and j, which is a consequence of MercerŌĆÖs theorem [10]. The entire process of training the model and generating predictions is simply carried out by using the kernel. The kernel plays a significant role in constructing SVM models, and various types of kernels are available, among which a linear kernel and a clinical kernel were considered. The linear kernel is given as k ( x i , ┬Ā x j ) ┬Ā = ┬Ā x i T x j k ( x i , ┬Ā x j ) ┬Ā = ┬Ā ( m a x - m i n ) - x i - x j m a x - m i n k ( x i , ┬Ā x j ) ┬Ā = ┬Ā 1 , ┬Ā i f ┬Ā x i ┬Ā = ┬Ā x j ┬Ā 0 , ┬Ā i f ┬Ā x i ┬Ā ŌēĀ ┬Ā x j
Although SVCR and RankSVMs share the same framework to a certain extent, they differ in terms of how they utilize information for their ultimate objective. SVCR is designed to directly predict the survival time and to minimize the absolute error between predicted and observed survival times. In contrast, RankSVMs focuses on predicting the correct ranking of survival times rather than predicting the actual survival time. In this respect, SVCR extends the standard support vector regression to censored data by penalizing incorrect predictions of censored observations [5,6], while RankSVMs takes into account the ranking problem for the censored data by minimizing the empirical risk of incorrectly ranking two observations.
All statistical analyses were done using R version 3.6.2 (The R Foundation for Statistical Computing, Vienna, Austria). The only continuous covariable, age, was reported as the mean ┬▒ standard deviation, and the other categorical variables were reported as frequencies with percentages, as shown in Table 1.
Two Kaplan-Meier survival curves were compared using the log-rank test, as shown in Fig. 2. In addition, 5-year survival rates and median survival times were given. Variables with p-values less than 0.05 in the univariate Cox model were entered into a multivariate Cox proportional hazards model to estimate the hazard ratios (HRs) for the corresponding predictors, as shown in Fig. 3.
For the implementation of RSF, the number of binary decision trees, the maximum variables for splitting in each node, and the splitting rules for measuring survival differences are shown in Table 2.
The number of trees was 50, 100, 200, 500, and 1,000, and the variables for splitting were given as 10. Although there were seven variables, three variables (histologic differentiation, AJCC 8th edition T-stage, and N-stage) had one more additional variable after one-hot encoding. Three different split rules were applied: log-rank splitting [12,13], gradient-based Brier score splitting [14], and log-rank score splitting [15]. As a result, 150 models for each dataset were constructed, consisting of a combination of the number of trees, the number of variables for splitting, and the split rules.
To implement SVM, 80 models were considered from combinations of various hyperparameters: two SVM models (SVCR and RankSVMs), two types of kernels (linear and clinical kernels), two ways of computing distance between data points (makediff1 and makediff3), and 10 values of the regularization parameter ╬│ as shown in Table 3. The two arguments makediff1 and makediff3 are used in the R package survivalsvm, in which makediff1 computes the distance between two consecutive observations only when the first one is not censored, whereas makediff3 computes the difference between data point i and its neighbor that has the largest survival time that is smaller than the survival time of y_i [8]. In total, 80 models were cross-validated and the model with the best validation C-index was chosen.
Based on three survival predictive models, we investigated personalized treatment policies using the survival rate over time. It is well known that the Cox model assumes a proportional HR over time, which implies that the HRs between different individuals are constant over time. However, the two ML models used in this study reflect more complex interactions between covariates and yield non-constant HRs between different individuals over time. For personalized treatment, it would be more desirable to predict the survival rate over time using the ML models than using the Cox model.
Fig. 2 shows the two Kaplan-Meier survival curves for the SEER and KOTUS-BP datasets. The censoring fractions were 30.7% for SEER and 49.5% for KOTUS-BP. These two survival curves overlapped for up to 20 months and then significantly separated, with a p-value less than 1e-13 from the log-rank test for the equivalence of two survival curves. The median survival times were 21 months for SEER and 24 months for KOTUS-BP. Fig. 3 shows the estimated HRs of each clinical variable from the multivariate Cox model with 95% confidence intervals and p-values for both datasets. The estimated HRs of the seven variables were not meaningfully different between the datasets, and all the variables were significant, except for sex in KOTUS-BP dataset.
Table 4 shows the C-index values and 1-year, 2-year, and 3-year time-dependent AUCs for the final Cox, RSF, and SVM survival analysis models according to the three schemes of model development. The Cox, RSF, and SVM models performed somewhat better when the two datasets were mixed half and half than when the first and second schemes were applied. Although the results are not shown here, the performance of RankSVMs was exceptionally low, with C-index values of 0.548, 0.529, and 0.514 for the three schemes, respectively. This implies that the rank-based approach performed worse than the regression-based approach in this study.
Through 10-fold CV of 150 RSF models, the model with the best validation Harrell C-index was chosen as the final RSF model. The final RSF model consisted of 100 decision trees, used a maximum of two variables in splitting nodes, and used the log-rank test to measure survival differences when two datasets were mixed half and half. The C-index and 1-year, 2-year, and 3-year time-dependent AUCs were 0.6337, 0.6824, 0.6681, and 0.6781, respectively.
Similarly, the model with the best validation Harrell C-index was chosen through 10-fold CV of 80 SVM models. The final SVM model was the SVCR model based on an additive clinical kernel, regularization constant (╬│) of 0.1, and the makediff3 method to calculate the distance between data points when the two datasets were mixed half and half. The C-index and 1-year, 2-year and 3-year time-dependent AUCs were 0.6233, 0.6849, 0.6352, and 0.6264, respectively.
The C-index and 1-year, 2-year, and 3-year time-dependent AUCs of the Cox model were 0.6434, 0.6976, 0.6795 and 0.6873, respectively. Comparing these values to those of the two ML survival models, the Cox model consistently performed slightly better than RSF and SVM models. The Cox model also yielded slightly better results when the two datasets were mixed half and half than when the two datasets were not mixed.
In order to consider personalized treatment policies, we compared the predictive survival curves of three different patients using the fitted Cox model and the final RSF model described above. Suppose that the three chosen patients (A, B, and C) are all 50-year-old women, have a tumor in the body or tail of the pancreas, and have not received chemotherapy. Patient A has a well differentiated tumor staged T1 and N0 according to the AJCC 8th edition staging system. Patient B has a moderately differentiated tumor staged T2 and N1, whereas patient C has a poorly differentiated tumor staged T3 and N2. We plotted two predicted survival curves from both the Cox model and RSF model for these three patients over time, as shown in Fig. 4. The predicted survival curves from the Cox model showed relatively consistent differences among these three patients over time, whereas those from the RSF model showed less consistent differences. For example, the slope of the survival curve of patient C suddenly changed at 10 months after the diagnosis and the slope of patient B dramatically changed at 17 months after the diagnosis, whereas the slope of patient A did not change over time. Therefore, it seems that there is a discrepancy between the survival curves generated using the Cox and RSF models. This may imply that different treatment strategies for different patients would maximize treatment efficacy.
In light of the development of a predictive survival model for PDAC [1], we considered a comparative study to investigate whether ML methods for survival analysis improve the predictability of the survival rate. In this study, both RSF and SVM methods for survival analysis were considered and compared with the Cox model [1] using the same SEER and KOTUS-BP datasets. In addition to the scheme used in the previous model [1], two other schemes were considered for model development and evaluation. In the second scheme, the roles of these two datasets were reversed, so that KOTUS-BP was used as the training set and SEER was used as the external validation set. In the third scheme, these two datasets were mixed half and half, and one of the mixed datasets was randomly chosen for model development and the remaining dataset was used for external validation. As shown in the Results section, the third scheme yielded slightly better performance for all methods than the other two schemes.
Compared with the Cox model, the performance of the ML survival models was not significantly improved, and RSF performed similarly to the Cox model. However, the performance of SVM differed substantially according to how the survival information was used. The performance of SVCR was comparable to those of the Cox model and RSF, since SVCR utilizes the survival time in the regression model considering the censoring mechanism. In contrast, the performance of RankSVMs was not good because this method only uses the ranking information of the survival times.
The RSF and SVM showed no substantial improvements in performance compared to the Cox model. In this study, only seven clinical variables were shared between the SEER and KOTUS-BP datasets, which might have been too few to maximize the usefulness of ML methods. ML methods are useful to analyze more complex and nonlinear associations among high-dimensional variables such as genetic information. It was also noted that the Harrell C-index of all models, both in the training set and in the test set, was less than 0.70, except for one or two cases.
Although it takes more time to develop ML survival models than a Cox model and there is no substantial performance improvement, these ML survival models have the advantage of allowing nonlinear risk to be predicted over time. As shown in Fig. 4, the trend in the survival curves for the RSF model was different from that for the Cox model. For example, the survival curves of the RSF model had the largest difference between patients B and C when 1 year to 2 years had passed. With this information, clinicians can pay particular attention to patient C in this period. Meanwhile, patients in a period with particularly high risk can be informed in advance, so that they could receive additional health care in that period. The fact that the RSF model outputs the survival curve of each individual might enable more patient-specific care. Furthermore, ML survival models recommend whether a patient should receive treatment or not [16]. Adjuvant chemotherapy was found to be helpful for almost all of the patients in this study, but other treatments can be rather harmful to some patients.
Notes
Acknowledgments
This work was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (2019R1F1A1062005) and a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (grant number: HI16C2037).
Fig.┬Ā1.
Flowchart of model development and external validation process for the Cox, random survival forests, and support vector machines models. SEER, Surveillance, Epidemiology and End Results; Cox PH, Cox proportional hazard; KOTUS-BP, Korea Tumor Registry System-Biliary Pancreas; CV, cross-validation.
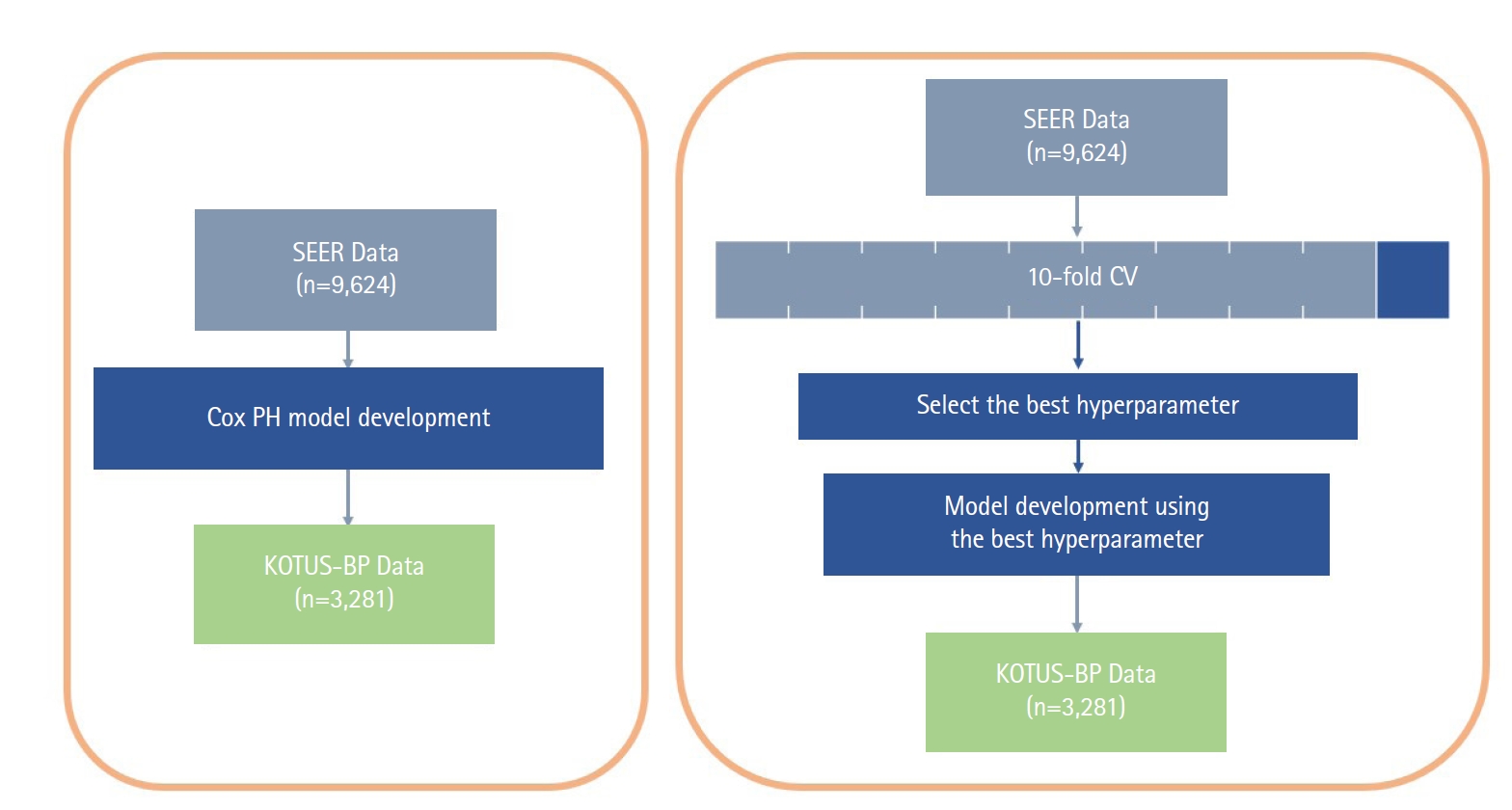
Fig.┬Ā2.
Kaplan-Meier survival curves with 5-year overall survival (OS) rates and median survival times for the Surveillance, Epidemiology and End Results (SEER) and Korea Tumor Registry System-Biliary Pancreas (KOTUS-BP) datasets.
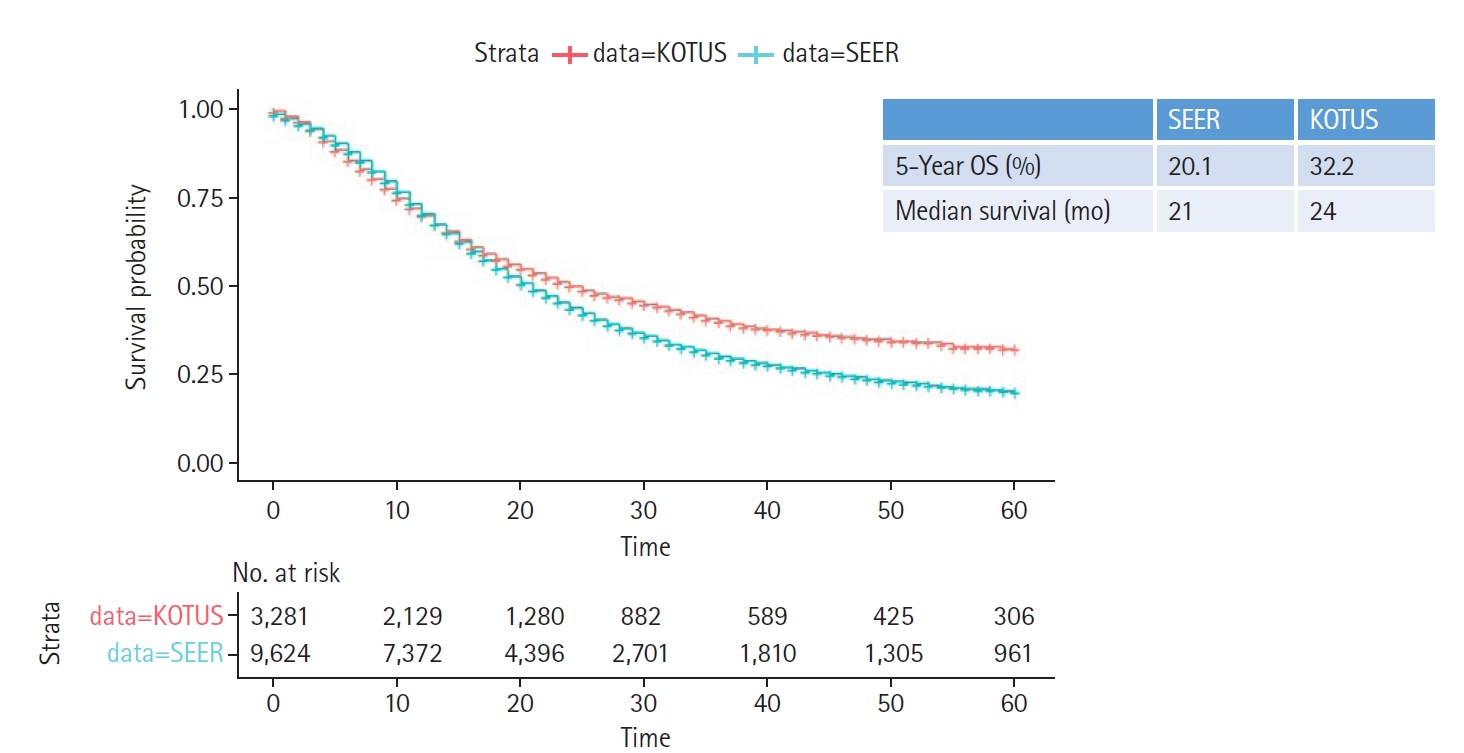
Fig.┬Ā3.
Hazard ratios and 95% confidence intervals of seven variables in the Surveillance, Epidemiology and End Results (SEER) and Korea Tumor Registry System-Biliary Pancreas (KOTUS-BP) datasets. AJCC, American Joint Committee on Cancer.
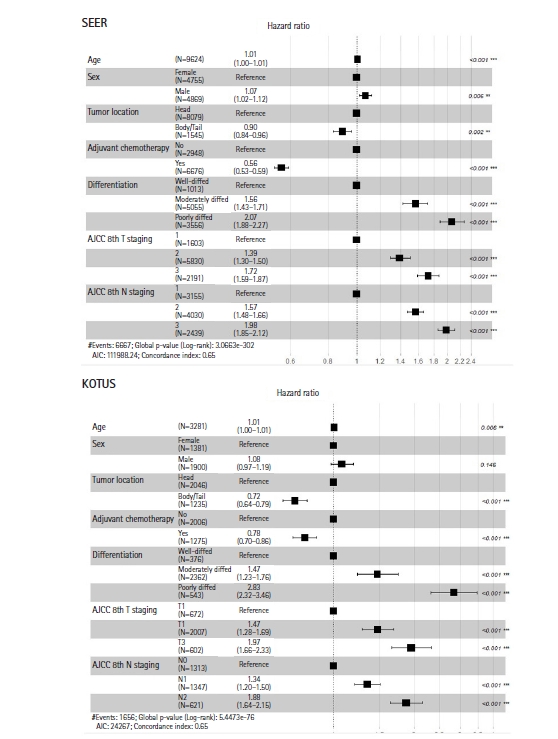
Fig.┬Ā4.
Overlaid predicted survival curves of the Cox model and random survival forests (RSF) method for three patients. Cox PH, Cox proportional hazard.

Table┬Ā1.
Basic statistics and 5-year overall survival rates for seven variables in the SEER and KOTUS-BP databases
| Variable | SEER database (n=9,624) | KOTUS database (n=3,281) | ||||
|---|---|---|---|---|---|---|
| Patients | 5-Year OS (%) | p-valuea | Patients | 5-Year OS (%) | p-valuea | |
| Age (yr) | 65.6┬▒10.4 | 20.1 | 63.8┬▒10.1 | 32.2 | ||
| Female | 4,755 (49.4) | 21.3 | 1,381 (42.1) | 36.2 | ||
| Male | 4,869 (50.6) | 18.9 | 0.006 | 1,900 (57.9) | 29.2 | 0.146 |
| Head | 8,079 (83.9) | 19.2 | 2,046 (62.4) | 28.5 | ||
| Body/Tail | 1,545 (16.1) | 25.0 | 0.002 | 1,235 (37.6) | 37.8 | <0.001 |
| No adjuvant treatment | 2,948 (30.6) | 17.3 | 2,006 (61.1) | 29.5 | ||
| Adjuvant treatment | 6,676 (69.4) | 21.3 | <0.001 | 1,275 (38.9) | 36.1 | <0.001 |
| Well differentiated | 1,013 (10.5) | 37.4 | 376 (11.5) | 44.9 | ||
| Moderately differentiated | 5,055 (52.5) | 20.5 | <0.001 | 2,362 (72.0) | 32.9 | <0.001 |
| Poorly differentiated | 3,556 (37.0) | 14.6 | <0.001 | 543 (16.5) | 20.8 | <0.001 |
| ŌĆāT1 | 1,603 (16.7) | 32.7 | 672 (20.5) | 45.3 | ||
| ŌĆāT2 | 5,830 (60.6) | 18.8 | <0.001 | 2,007 (61.2) | 29.7 | <0.001 |
| ŌĆāT3 | 2,191 (22.7) | 14.3 | <0.001 | 602 (18.3) | 24.5 | <0.001 |
| ŌĆāN0 | 3,155 (32.8) | 32.4 | 1,313 (40.0) | 42.6 | ||
| ŌĆāN1 | 4,030 (41.9) | 20.5 | <0.001 | 1,347 (41.1) | 28.5 | <0.001 |
| ŌĆāN2 | 2,439 (25.3) | 14.6 | <0.001 | 621 (18.9) | 16.4 | <0.001 |
Table┬Ā2.
Hyperparameters for random survival forests
| Hyperparameter | Value |
|---|---|
| No. of trees | 50, 100, 200, 500, 1,000 |
| Max. variables used in split | 1ŌĆÆ10 |
| Splitting rule | log-rank/bs.gradient/logrankscore |
Table┬Ā3.
Hyperparameters for support vector machines for survival analysis
| Hyperparameter | Value |
|---|---|
| SVM type | SVRC, RankSVMs |
| Kernel | Linear, clinical |
| Distance matrix | Makediff1, makediff3 |
| Regularization constant | 0.01, 0.02, 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10 |
Table┬Ā4.
C-index and 1-year, 2-year, 3-year time-dependent AUCs for the Cox, RSF, and SVM models according to three schemes
AUC, area under receiver operating characteristic curve; RSF, random survival forests; SVM, support vector machines; C-index, HarrellŌĆÖs concordance index; Td1, 1-year time-dependent; Td2, 2-year time-dependent; Td3, 3-year time-dependent; KoTUS, Korea Tumor Registry System-Biliary Pancreas; SEER, Surveillance, Epidemiology and End Results.
References
1. Kang JS, Mok L, Heo JS, Han IW, Shin SH, Yoon YS, et al. Development and external validation of survival prediction model for pancreatic cancer using two nationwide databases: Surveillance, Epidemiology and End Results (SEER) and Korea Tumor Registry System-Biliary Pancreas (KOTUS-BP). Gut Liver 2021;15:912ŌĆō921.



2. Hothorn T, Lausen B, Benner A, Radespiel-Troger M. Bagging survival trees. Stat Med 2004;23:77ŌĆō91.


3. Ishwaran H, Kogalur UB, Blackstone EH, Lauer MS. Random survival forests. Ann Appl Stat 2008;2:841ŌĆō860.

4. Ishwaran H, Kogalur UB, Chen X, Minn AJ. Random survival forests for high-dimensional data. Stat Anal Data Mining ASA Data Sci J 2011;4:115ŌĆō132.


5. Shivaswamy PK, Chu W, Jansche M. A support vector approach to censored targets. In: In: 7th IEEE International Conference on Data Mining (ICDM 2007), 2007 Oct 28-31; Omaha, NE, USA: New York: Institute of Electrical and Electronics Engineers, 2008. pp 655ŌĆō660.

6. Khan FM, Zubek VB. Support vector regression for censored data (SVRc): a novel tool for survival analysis. In: In: 8th IEEE International Conference on Data Mining, 2008 Dec 15-19; Pisa, Italy: New York: Institute of Electrical and Electronics Engineers, 2009. pp 863ŌĆō868.

7. Van Belle V, Pelckmans K, Suykens JA, Van Huffel S. Support vector machines for survival analysis. In: In: Proceedings of the Third International Conference on Computational Intelligence in Medicine and Healthcare (CIMED2007), 2007 Jul 25-27; Plymouth, UK: pp 1ŌĆō8.
8. Van Belle V, Pelckmans K, Van Huffel S, Suykens JA. Support vector methods for survival analysis: a comparison between ranking and regression approaches. Artif Intell Med 2011;53:107ŌĆō118.


9. De Bin R. Boosting in Cox regression: a comparison between the likelihood-based and the model-based approaches with focus on the R-packages CoxBoost and mboost. Technical report number 180. Munchen: University of Munich, 2015.
10. Herbrich R, Graepel T, Obermayer K. Large margin rank boundaries for ordinal regression. In: Advances in Large Margin Classifiers (Smola A, Bertlett P, Scholkopf B, Schuurmans D, eds.). Cambridge: MIT Press, 2000. pp. 115ŌĆō132.
11. Daemen A, De Moor B. Development of a kernel function for clinical data. Annu Int Conf IEEE Eng Med Biol Soc 2009;2009:5913ŌĆō5917.


14. Brier GW. Verification of forecasts expressed in terms of probability. Monthly Weather Rev 1950;78:1ŌĆō3.

- TOOLS
-
METRICS

-
- 5 Crossref
- 0 Scopus
- 4,877 View
- 163 Download
- Related articles in GNI








