Comparison of Two Meta-Analysis Methods: Inverse-Variance-Weighted Average and Weighted Sum of Z-Scores

Article information

Genomics Inform. 2016;14(4):173-180

Publication date (electronic) : 2016 December 30

doi : https://doi.org/10.5808/GI.2016.14.4.173

Cue Hyunkyu Lee ¹^,², Seungho Cook ¹^,³, Ji Sung Lee ¹^,⁴, Buhm Han ¹^,²

¹Asan Institute for Life Sciences, Asan Medical Center, Seoul 05505, Korea.

²Department of Convergence Medicine, University of Ulsan College of Medicine, Seoul 05505, Korea.

³School of Systems Biomedical Science, Soongsil University, Seoul 06978, Korea.

⁴Department of Medicine, University of Ulsan College of Medicine, Seoul 05505, Korea.

Corresponding author: Tel: +82-2-3010-4176, Fax: +82-2-3010-4182, buhm.han@amc.seoul.kr

Received 2016 October 18; Revised 2016 December 03; Accepted 2016 December 03.

Abstract

The meta-analysis has become a widely used tool for many applications in bioinformatics, including genome-wide association studies. A commonly used approach for meta-analysis is the fixed effects model approach, for which there are two popular methods: the inverse variance-weighted average method and weighted sum of z-scores method. Although previous studies have shown that the two methods perform similarly, their characteristics and their relationship have not been thoroughly investigated. In this paper, we investigate the optimal characteristics of the two methods and show the connection between the two methods. We demonstrate that the each method is optimized for a unique goal, which gives us insight into the optimal weights for the weighted sum of z-scores method. We examine the connection between the two methods both analytically and empirically and show that their resulting statistics become equivalent under certain assumptions. Finally, we apply both methods to the Wellcome Trust Case Control Consortium data and demonstrate that the two methods can give distinct results in certain study designs.

Keywords: fixed effects model; genome-wide association study; inverse variance-weighted average; meta-analysis; optimality; weighted sum of z-scores

Introduction

The meta-analysis is a tool for pooling information from multiple independent studies [1 2 3 4]. In the field of genetics, the meta-analysis has become a popular way of aggregating information from multiple genome-wide association studies (GWASs) in order to increase statistical power while controlling for the rate of false positive findings [5 6 7 8 9 10 11 12 13]. The meta-analysis has also become a useful tool for many applications of bioinformatics, such as neuroimage processing [14] and expression quantitative trait loci analysis [15].

There exist several approaches for combining information from multiple studies. Statistical methods can differ depending on the scenario: when (1) test statistics are unknown but only p-values are available, (2) test statistics are known but data are not available, or (3) actual data are available. In this paper, we focus on scenario (2), which is a common situation in genetic studies. We note that for scenario (1), Fisher's method for combining p-values is commonly used [16]. In scenario (3), we can combine actual data, which is rarely doable in retrospective studies or in genetic studies where transferring genotype data is difficult due to privacy issues. For scenario (2), which we focus on, the fixed effects model meta-analysis is the most common approach for synthesizing test statistics from multiple studies [1 17].

To perform a fixed effects model meta-analysis, there are two popular methods: the inverse variance-weighted average and the weighted sum of z-scores (SZ) [2 17 18]. The inverse variance-weighted average method (IVW) summarizes effect sizes from multiple independent studies by calculating the weighted mean of the effect sizes using the inverse variance of the individual studies as weights. The weighted SZ method constructs a new z-score by calculating a weighted sum of individual z-scores. It has been known that the sample size of individual studies is a preferable weight for the method [10 19 20]. Although several empirical evidence has shown that the two methods perform similarly [2 17 21], the characteristics of each method and the analytical connection between the two methods have not been thoroughly investigated.

In this paper, we first investigate the optimal characteristics of the two methods. We show that the two methods are optimized for different optimality criteria: IVW maximizes the likelihood function, which is equivalent to minimizing the estimator variance, and SZ maximizes the non-centrality parameter of the statistic, which is equivalent to maximizing the statistical power. This characterization gives us insight into the optimal weight for SZ; using only the sample size information as weights can often be suboptimal in terms of statistical power compared with using all information as weights, such as minor allele frequencies. Although the two methods are optimized for different goals, we analytically demonstrate that the two methods become equivalent under certain assumptions that hold over a wide range of applications. We examine this connection between the two methods both analytically and empirically. Finally, using real data analysis utilizing the Wellcome Trust Case Control Consortium data, we demonstrate that the two methods can give distinct results in certain study designs.

Methods

Inverse variance-weighted average method

We first describe the two methods for the fixed effects model meta-analysis: the IVW and weighted SZ. The fixed effects model assumes that all studies in a meta-analysis share a single true effect size [2 18 22 23]. The underlying mathematical model of the observed effect X_i can be shown as:

X_i = µ + e_i, (1)

where µ is the true effect size and ei (the deviation of X_i from µ) is the error in the observation and i = 1,2,…,C. In order to integrate multiple observed effect sizes X₁,…,X_C from multiple studies, the weighted mean approach has been suggested [22],

X¯=∑WiXi∑Wi

. (2)

A choice of weight W_i is not immediately evident, but several attempts were made to identify the optimal weight of the methods based on empirical evidence [17 20 24]. Ideally, one needs to put more weight on the studies with more precision against studies with lower precision [3 25 26]. When the sample size of each study is sufficiently large, we can assume that X_i follows a normal distribution approximately, based on the central limit theorem. This applies to situations where the data themselves are not normal (e.g., binary), in which situation the test statistic still follows a normal distribution, as long as the sample size is large. In GWASs, this assumption holds easily, because the sample size is typically as large as thousands of samples. Note that all derivations in this paper are based on this normality assumption. Let SE(X_i) be the estimated standard error of X_i, and V_i = SE(X_i)². It is common practice to consider the estimated variance V_i as the true variance. The inverse variance-weighted average effect size estimator is the weighted mean of X_i with the weights [22]:

W_i = V_i⁻¹. (3)

Given these weights, the standard error of the average effect size 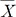X¯ becomes 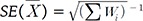SEX¯=∑Wi−1. The statistical significance can be tested by constructing a z-score statistic of IVW as follows, which asymptotically follows N(0,1) under the null hypothesis of no effects.

ZIVW=X¯SE(X¯)=∑WiXi∑Wi

(4)

The p-value of the two-tailed significance test is

p = 2Φ(−|Z_IVW|), (5)

where Φ is the standard normal cumulative distribution function.

Weighted SZ

Another popular method for the fixed effects model meta-analysis is calculating the weighted SZ from the follows studies. Let Z_i be the z-score from study i, whichN(0,1) under the null hypothesis of no effects. Then, the weighted SZ statistic is

ZSZ=∑wSZ, iZi∑wSZ, i2

. (6)

By the characteristic of a normal distribution, Z_SZ also follows N(0,1) under the null hypothesis. To combine z-scores from multiple studies, a per-study sample size was suggested as weights of each study, as follows [2 10]:

wSZ, i=Ni

, (7)

where N_i is sample size of the study.

Results

Below, we show the characteristics of the two methods and the connections between the two methods. We first show that each method is optimized to meet a unique optimality criterion. Then, we show that the two methods are connected, by using both analytical derivations and empirical simulations. Finally, we demonstrate a situation in which the two methods can give different results using real data.

Optimality of IVW

IVW maximizes likelihood function

We will define that a method is optimal if the method achieves a specific goal more effectively than any other method. We show that IVW is optimal in two different aspects: (1) the summary estimator gives the greatest likelihood than any other estimator and (2) the summary estimator's variance is smaller than the variance of any other estimator. First, we show that IVW is optimal in the sense that the IVW estimator maximizes the likelihood function. Suppose that we have a series of n studies with observed effect sizes X_i, i = 1, 2, … n. Under the fixed effects assumption, there exists a true effect size µ, and each observation X_i comes from a normal distribution with mean µ and a standard deviation σ_i. The probability density function of each observation is given by

fXi|µ, σi2=12πσi2e−Xi−µ22σi2

. (8)

Because −lnL(µ,σ_i²|X₁,…,X_n) will be minimized at 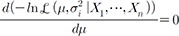d(−lnLµ, σi2X1, …, Xn)dµ=0 , we can obtain the maximum likelihood (ML) estimator:

µ^=∑i=1nσi2−1Xi∑i=1nσi2−1

, (9)

which is equivalent to the IVW statistic X¯

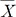in equation (2). Therefore, the inverse variance-weighted average method is optimal in the sense that it maximizes the likelihood of observations with the optimized weight of W_i = (σ_i²)⁻¹ [21 22].

IVW achieves minimum variance

IVW is optimal in the sense that the IVW estimator achieves minimum variance. In short, IVW achieves minimum variance by the properties of maximum likelihood estimator (MLE). MLE has the following property, as shown by Greene [27]: if the sampling is from an exponential family of distributions and the minimum variance unbiased estimator (MVUE) exists, that estimator becomes the ML estimator [27]. Thus, by this property and under these conditions, we can conclude that IVW achieves minimum variance, because IVW is the MLE and MVUE [27].

Optimality of SZ

SZ maximizes the non-centrality parameter

SZ combines z-scores from multiple studies to construct a new z-score. Therefore, in SZ, we are not interested in the estimator of X_i. Rather, we are interested in the statistical significance of the combined information. Thus, the goal of SZ is to maximize how much the z-score will be shifted from 0 on average, which is often called the non-centrality parameter. By maximizing the non-centrality parameter, we can maximize the statistical power of the test. Among all possible weights that can construct a weighted SZ, we want to find the weights that will maximize the non-centrality parameter.

The optimal weights of the weighted SZ can be found by the Cauchy-Schwarz inequality. We will make an assumption that

Zi=Xi/Vi

. (10)

That is, we assume that our z-score is defined as the effect size estimate divided by the standard error, which is the common definition of a z-score. In some applications, there can be different ways to define a z-score statistic, and for those definitions, the connection between z-score and effect size may not be apparent. However, in practice, this assumption holds approximately over a wide range of applications. Below, we will show that in the situation of a 2 × 2 table, even if we obtain a z-score in a different way, it approximates a z-score that is obtained by using effect size and its standard error.

Under the fixed effect model assumption that assumes E[X_i] = µ, the z-score, Z_i, follows a normal distribution Z_SZ~N(λ,1), where λ is a non-centrality parameter with 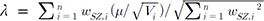λ=∑i=1nwSZ, i(µ/Vi)/∑i=1nwSZ, i2. Now, we want to obtain the weight wi that maximizes lambda. The optimal weight can be obtained by using the Cauchy-Schwarz inequality, as follows [12 21]:

λ=∑i=1nwSZ, i∑i=1nwSZ, i2•1Vi≤µ∑i=1nwSZ, i2∑i=1nwSZ, i2∑i=1n1Vi

. (11)

The equality is achieved when

wSZ, i∑i=1nwSZ, i2=k•1Vi

, (12)

where the terms ∑i=1nwSZ, i2

and k are constants. Thus, the optimal weight is wSZ, i=1/Vi

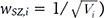. Then, the resulting weighted SZ can be constructed as

ZSZ=∑i=1nSEXi−1Zi∑i=1nSEXi−2

. (13)

This result provides us with the intuition that SZ is optimal only when we weight z-scores by the inverse of the standard errors of effect sizes. That is why previous studies have weighted z-scores by 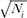Ni, because in many applications, the variance V_i is inversely proportional to the sample size N_i. However, we would like to note that in some applications, the variance can be a function of not only N_i but also other properties of the data. For example, in genetic association studies, when we test an association of a single-nucleotide polymorphism (SNP) to a phenotype, the variance is typically inversely proportional to N_ip_i(1−p_i), where p_i denotes the allele frequency of the risk allele. This suggests that if the datasets that we want to combine have different allele frequencies, weighting the z-scores only by N_i can be suboptimal. Below, we will show by simulations that we can have some power loss by using just N_i as the weight, instead of accounting for frequency differences. However, the approximation of this weight 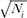Ni will be optimal when no heterogeneity can be found between the minor allele frequencies [2].

Equality of IVW and SZ under certain assumptions

Analytical derivation

Here, we show that the two methods IVW and SZ are equivalent under certain assumptions. We have shown that IVW is optimal in the sense that the estimator is MLE and achieves minimum variance, and SZ is optimal in the sense that it maximizes the non-centrality parameter. Although both methods can be considered optimal, their goals and how they are optimized are completely different; IVW aims to obtain the best summary estimate (thus MLE and minimum variance), and SZ aims to maximize the statistical power, without considering the summary estimator. Despite the fact that the two methods are optimized differently with different goals, we show that the resulting statistics are equivalent, in the sense that their z-scores (and therefore their p-values) are equivalent. Again, we assume the definition of z-score Zi=XiVi, which is assumed in Eq. (18). We assume that SZ uses SE(X_i)⁻¹ as weights for z-scores, rather than only using sample sizes.

Then, we can show, by simple algebra:

ZSZ=∑iSEXi−1Zi∑iSEXi−2=∑iWiXi∑iWi=ZIVW

, (14)

which demonstrates that the two methods are exactly equivalent if we use SE(X_i)⁻¹ as weights for SZ.

Empirical simulation

To empirically investigate the equality of IVW and SZ, we compared the power of the two methods. We assumed the following null and alternative hypotheses:

H₀:µ = 0

H₁:µ ≠ 0

That is, we tested if the mean effect is non-zero.

To generate simulation sets of meta-analysis studies, we used the common simulation framework for simulating genetic association studies. We assumed that there is a single SNP whose minor allele confers risk of a disease, which is a dichotomous trait. We assumed a number of different relative risks, 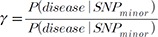γ=PdiseaseSNPminorPdiseaseSNPminor, ranging from 1.01 to 1.2. We assumed a meta-analysis of 5 genetic association studies and assumed a minor allele frequency (MAF) of 0.3. In an additional simulation setting, we assumed varying MAFs of (0.1,0.2,0.3,0.4,0.5) for the 5 studies. We assumed a very small disease prevalence (F ≈ 0). Given these assumptions and parameters, we can calculate the expected MAF in cases and in controls. Specifically, given MAF p and relative risk γ, the case MAF becomes γp/((γ−1)p + 1), where the control MAF becomes approximately p, given F ≈ 0. Given the expected MAF in cases and controls, we could randomly sample genotype data, assuming 500 cases and 500 controls for each of the five studies. To assess the statistical significance of the sample data, we used log odds ratio as a statistic, which follows an asymptotic normal distribution. We repeated the procedure to generate 100,000 simulated meta-analysis sets. Given the significance level α = 0.05, the power was the proportion of sample sets whose meta-analysis p-value was ≤α.

We compared the two methods—IVW and weighted SZ—using the inverse standard error as a weight factor (SZ_SE). Fig. 1 shows that the two methods showed the same power in both situations: under no heterogeneity in MAF between studies (Fig. 1A) and under heterogeneity in MAF (Fig. 1B). This result complements our analytical results that the two methods are equivalent if SZ uses SE(X_i)⁻¹ as weights.

Fig. 1

Power test of IVW, SZ_SE, and SZ_N. Total 100,000 simulated meta-analysis data sets of five studies were generated, each with 500 case and 500 control. (A) We assumed the same MAFs of 0.3 for five studies. (B) We assumed varying MAFs of 0.1, 0.2, 0.3, 0.4, and 0.5 for five studies. IVW, inverse variance-weighted average method; SZ_SE, weighted SZ whose weights are given as inverse standard error; SZ_N, SZ whose weights are given as the square root of sample size; MAF, minor allele frequency.

Additionally, we compared the two methods with another method, the weighted SZ, which uses the inverse squared root sample size as the weight (SZ_N). SZ_N was equivalent to IVW and SZ_SE in terms of power, when there was no heterogeneity in MAF (Fig. 1A). However, with the existence of differences in allele frequencies (therefore, differences in weights, w_IVW,i ≠ w_{SZ_N,i}), SZ_N showed a slight power loss from the other two methods (Fig. 1B). This result demonstrates that using only sample size as the weight can be suboptimal if there are other factors that can cause variance differences between studies, such as allele frequencies. Nevertheless, the power drop of using only sample size as the weight was quite small (i.e., at γ = 1.15, the power of IVW and SZ_SE was 58.24%, but the power of SZ_N was 57.23%, with only 1.01% power loss.)

Situations in which IVW and SZ can give distinct results

In this section, we demonstrate a situation in which IVW and SZ can give distinct results. As we have shown above, SZ whose weights are given as SE(X_i)⁻¹(SZ_SE) is analytically equivalent to IVW. However, SZ whose weights are given as the square root of sample size (SZ_N) can give slightly different results, if the expected relationship SEXi−1∝N is broken. We have already shown that a MAF difference can result in such breakage of this relationship. Here, additionally, we show that the use of a linear mixed model can also result in such breakage of the relationship SEXi−1∝N. We used the data of the Wellcome Trust Case Control Consortium [28]. This dataset includes approximately 2,000 cases for each of seven different diseases and 1,500 controls for each of two control groups (1958C and National Bureau of Standards [NBS]). We used the data on rheumatoid arthritis (RA) and type 1 diabetes (T1D). After standard quality-control and removal of the MHC region, we obtained 469,225 SNPs. We performed association tests for two diseases; we performed association tests for RA using NBS as controls and association tests for T1D using 1958C as controls. The sample sizes for the two association tests were similar (N = 3,318 and 3,443, respectively). We used logistic regression implemented in plink (with--logistic command). Because the sample sizes of the two tests were similar, we expected that for each SNP, the standard errors of the effect size estimate would be similar. That is, we wanted to test if the relationship SEXi−1∝N held well for these real data. Fig. 2A shows that when we plotted the log10 value of the ratio of the two standard errors, the values were highly concentrated around 0. This implies that the standard errors were very similar between RA and T1D, as expected, because the sample sizes were similar. Thus, the relationship SEXi−1∝N approximately held well. Therefore, Fig. 2A shows that IVW and SZ_N have similar results in this situation.

Fig. 2

Ratio of standard errors of RA and T1D association analyses. Left panel shows log10 values of the ratio of the two standard errors from the two studies participating in a meta-analysis (RA and T1D). Right panel shows the −log10 values of p-values of two different meta-analysis methods (IVW and SZ_N) for combining the two studies (RA and T1D). (A) Both RA and T1D analyses used logistic regression. (B) Both RA and T1D analyses used linear mixed model using GEMMA. (C) RA analysis used linear mixed model and T1D analysis used logistic regression. RA, rheumatoid arthritis; T1D, type 1 diabetes; IVW, inverse variance-weighted average method; SZ_N, SZ whose weights are given as the square root of sample size.

Next, we changed the study design and used the linear mixed model implemented in the software package Genome-wide Efficient Mixed Model Association (GEMMA). We used GEMMA for both T1D and RA. Fig. 2B shows that the standard errors of these two analyses were similar. Then, we used GEMMA for T1D but not for RA. When we plotted the log10 value of the ratio of the resulting standard errors, the values deviated dramatically from 0 (Fig. 2C). The standard errors were much smaller in the linear mixed model than in the logistic regression. This is expected, because the effect sizes of the linear mixed model and logistic model have different meanings and are not comparable. Therefore, the relationship SEXi−1∝N does not hold. As a result, in the meta-analysis, the p-values of IVW and SZ_N differed dramatically. Note that the standard errors given by GEMMA can be slightly different from the standard linear model, because GEMMA regresses the effect of population structure. However, an additional analysis comparing the standard errors of GEMMA and the standard linear model demonstrated that this effect is minimal and that their standard errors were similar (Fig. 3). Thus, the difference observed between GEMMA and the logistic regression model was mainly due to the use of different models (linear and logistic).

Fig. 3

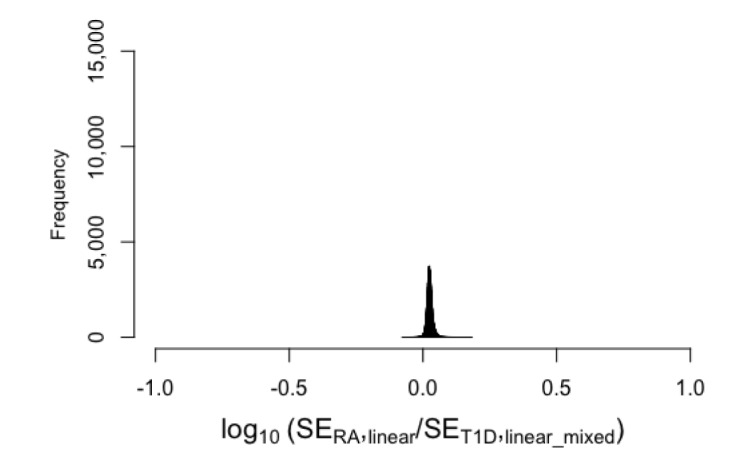
Ratio of standard errors of RA and T1D association analyses, when RA analysis used the standard linear regression and T1D analysis used linear mixed model. RA, rheumatoid arthritis; T1D, type 1 diabetes; SE, standard error.

One may argue that a meta-analysis design that combines the results of a logistic regression model and linear model is uncommon. Indeed, for binary traits, the use of a logistic regression model is more suitable. However, for dealing with population structure and cryptic relatedness, a linear mixed model is currently the main tool. For GWASs, there is no widely used efficient package implementing a logistic mixed model. For this reason, many studies are using a linear mixed model for binary traits as approximations. Therefore, if we assume a situation that the effect size in one study is obtained from a logistic regression model and the effect size in another study is obtained from a linear mixed model, the results of IVW and SZ_N can be different.

Discussion

In this paper, we investigated the optimal characteristics of two fixed effects meta-analysis methods: the inverse variance-weighted average and the weighted SZ. We showed that the two methods are optimized with different goals, but they are equivalent under certain assumptions. By analytical derivations and empirical simulations, we demonstrated their equivalency and provided insights into the optimal weights for the weighted SZ.

We have also shown that the optimal weights for the weighted SZ can be a function of not only the sample size but also other properties—for example, allele frequencies in GWASs. We empirically showed that if allele frequencies differ between studies, using only sample size for the weight can be suboptimal in terms of power. Therefore, we suggest that one should use effect size and standard error to define a z-score and use the inverse of the standard error as the weight for the weighted SZ. The standard error term includes all information, such as sample size and allele frequencies, thus providing optimal performance. Nevertheless, in our simulations, using just sample size resulted in only slightly lower power (at most, 1.07% power loss). Thus, in most applications, using only sample size for weights might perform reasonably well.

We also demonstrated that in some situations, the two meta-analysis methods can give different results. Specifically, when one study used the linear mixed model to account for population structure, the effect size from the linear mixed model can be incompatible with the effect size from the logistic regression model. In such situations, the use of meta-analysis methods based on z-scores or p-values is recommended, because it is not sensible to apply inverse variance-weighted average to multiple incompatible effect sizes from different statistical models.

Acknowledgments

This work was supported by a National Research Foundation of Korea (NRF) grant, funded by the Korean government (MSIP) (No. 2016R1C1B2013126).

References

1. Evangelou E, Ioannidis JP. Meta-analysis methods for genome-wide association studies and beyond. Nat Rev Genet 2013;14:379–389. 23657481.

2. de Bakker PI, Ferreira MA, Jia X, Neale BM, Raychaudhuri S, Voight BF. Practical aspects of imputation-driven meta-analysis of genome-wide association studies. Hum Mol Genet 2008;17:R122–R128. 18852200.

3. Zeggini E, Ioannidis JP. Meta-analysis in genome-wide association studies. Pharmacogenomics 2009;10:191–201. 19207020.

4. Cantor RM, Lange K, Sinsheimer JS. Prioritizing GWAS results: a review of statistical methods and recommendations for their application. Am J Hum Genet 2010;86:6–22. 20074509.

5. Borenstein M, Hedges LV, Higgins JP, Rothstein HR. A basic introduction to fixed-effect and random-effects models for meta-analysis. Res Synth Methods 2010;1:97–111. 26061376.

6. Zeggini E, Weedon MN, Lindgren CM, Frayling TM, Elliott KS, Lango H, et al. Replication of genome-wide association signals in UK samples reveals risk loci for type 2 diabetes. Science 2007;316:1336–1341. 17463249.

7. Traylor M, Mäkelä KM, Kilarski LL, Holliday EG, Devan WJ, Nalls MA, et al. A novel MMP12 locus is associated with large artery atherosclerotic stroke using a genome-wide age-at-onset informed approach. PLoS Genet 2014;10:e1004469. 25078452.

8. Lee MN, Ye C, Villani AC, Raj T, Li W, Eisenhaure TM, et al. Common genetic variants modulate pathogen-sensing responses in human dendritic cells. Science 2014;343:1246980. 24604203.

9. Raj T, Rothamel K, Mostafavi S, Ye C, Lee MN, Replogle JM, et al. Polarization of the effects of autoimmune and neurodegenerative risk alleles in leukocytes. Science 2014;344:519–523. 24786080.

10. Zaitlen N, Eskin E. Imputation aware meta-analysis of genome-wide association studies. Genet Epidemiol 2010;34:537–542. 20717975.

11. Zeggini E, Scott LJ, Saxena R, Voight BF, Marchini JL, Hu T, et al. Meta-analysis of genome-wide association data and large-scale replication identifies additional susceptibility loci for type 2 diabetes. Nat Genet 2008;40:638–645. 18372903.

12. Furlotte NA, Kang EY, Van Nas A, Farber CR, Lusis AJ, Eskin E. Increasing association mapping power and resolution in mouse genetic studies through the use of meta-analysis for structured populations. Genetics 2012;191:959–967. 22505625.

13. Nalls MA, Pankratz N, Lill CM, Do CB, Hernandez DG, Saad M, et al. Large-scale meta-analysis of genome-wide association data identifies six new risk loci for Parkinson's disease. Nat Genet 2014;46:989–993. 25064009.

14. Goodkind M, Eickhoff SB, Oathes DJ, Jiang Y, Chang A, Jones-Hagata LB, et al. Identification of a common neurobiological substrate for mental illness. JAMA Psychiatry 2015;72:305–315. 25651064.

15. Sul JH, Han B, Ye C, Choi T, Eskin E. Effectively identifying eQTLs from multiple tissues by combining mixed model and meta-analytic approaches. PLoS Genet 2013;9:e1003491. 23785294.

16. Fisher RA. Statistical Methods for Research Workers Edinburgh: Oliver and Boyd; 1925.

17. Han B, Eskin E. Random-effects model aimed at discovering associations in meta-analysis of genome-wide association studies. Am J Hum Genet 2011;88:586–598. 21565292.

18. Fleiss JL. The statistical basis of meta-analysis. Stat Methods Med Res 1993;2:121–145. 8261254.

19. Liptak T. On the combination of independent events. Magyar Tud Akad Mat Kutato Int Kozl 1958;3:171–197.

20. Zaykin DV. Optimally weighted Z-test is a powerful method for combining probabilities in meta-analysis. J Evol Biol 2011;24:1836–1841. 21605215.

21. Zhou B, Shi J, Whittemore AS. Optimal methods for meta-analysis of genome-wide association studies. Genet Epidemiol 2011;35:581–591. 21922536.

22. Cochran WG. The combination of estimates from different experiments. Biometrics 1954;10:101–129.

23. Mantel N, Haenszel W. Statistical aspects of the analysis of data from retrospective studies of disease. J Natl Cancer Inst 1959;22:719–748. 13655060.

24. Won S, Morris N, Lu Q, Elston RC. Choosing an optimal method to combine P-values. Stat Med 2009;28:1537–1553. 19266501.

25. Birch MW. The detection of partial association, I: the 2 × 2 case. J R Stat Soc Series B 1964;26:313–324.

26. Pereira TV, Patsopoulos NA, Salanti G, Ioannidis JP. Discovery properties of genome-wide association signals from cumulatively combined data sets. Am J Epidemiol 2009;170:1197–1206. 19808636.

27. Greene WH. Econometric Analysis Harlow: Pearson Education; 2011.

28. Wellcome Trust Case Control Consortium. Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature 2007;447:661–678. 17554300.

Article information Continued

(open-access, http://creativecommons.org/licenses/by-nc/4.0/) :

It is identical to the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/).