1. Evangelou E, Ioannidis JP. Meta-analysis methods for genome-wide association studies and beyond. Nat Rev Genet 2013;14:379ŌĆō389. PMID:
23657481.


2. de Bakker PI, Ferreira MA, Jia X, Neale BM, Raychaudhuri S, Voight BF. Practical aspects of imputation-driven meta-analysis of genome-wide association studies. Hum Mol Genet 2008;17:R122ŌĆōR128. PMID:
18852200.



3. Zeggini E, Ioannidis JP. Meta-analysis in genome-wide association studies. Pharmacogenomics 2009;10:191ŌĆō201. PMID:
19207020.



4. Cantor RM, Lange K, Sinsheimer JS. Prioritizing GWAS results: a review of statistical methods and recommendations for their application. Am J Hum Genet 2010;86:6ŌĆō22. PMID:
20074509.



5. Borenstein M, Hedges LV, Higgins JP, Rothstein HR. A basic introduction to fixed-effect and random-effects models for meta-analysis. Res Synth Methods 2010;1:97ŌĆō111. PMID:
26061376.


6. Zeggini E, Weedon MN, Lindgren CM, Frayling TM, Elliott KS, Lango H,
et al. Replication of genome-wide association signals in UK samples reveals risk loci for type 2 diabetes. Science 2007;316:1336ŌĆō1341. PMID:
17463249.



7. Traylor M, M├żkel├ż KM, Kilarski LL, Holliday EG, Devan WJ, Nalls MA,
et al. A novel MMP12 locus is associated with large artery atherosclerotic stroke using a genome-wide age-at-onset informed approach. PLoS Genet 2014;10:e1004469. PMID:
25078452.



8. Lee MN, Ye C, Villani AC, Raj T, Li W, Eisenhaure TM,
et al. Common genetic variants modulate pathogen-sensing responses in human dendritic cells. Science 2014;343:1246980. PMID:
24604203.



9. Raj T, Rothamel K, Mostafavi S, Ye C, Lee MN, Replogle JM,
et al. Polarization of the effects of autoimmune and neurodegenerative risk alleles in leukocytes. Science 2014;344:519ŌĆō523. PMID:
24786080.



10. Zaitlen N, Eskin E. Imputation aware meta-analysis of genome-wide association studies. Genet Epidemiol 2010;34:537ŌĆō542. PMID:
20717975.



11. Zeggini E, Scott LJ, Saxena R, Voight BF, Marchini JL, Hu T,
et al. Meta-analysis of genome-wide association data and large-scale replication identifies additional susceptibility loci for type 2 diabetes. Nat Genet 2008;40:638ŌĆō645. PMID:
18372903.



12. Furlotte NA, Kang EY, Van Nas A, Farber CR, Lusis AJ, Eskin E. Increasing association mapping power and resolution in mouse genetic studies through the use of meta-analysis for structured populations. Genetics 2012;191:959ŌĆō967. PMID:
22505625.



13. Nalls MA, Pankratz N, Lill CM, Do CB, Hernandez DG, Saad M,
et al. Large-scale meta-analysis of genome-wide association data identifies six new risk loci for Parkinson's disease. Nat Genet 2014;46:989ŌĆō993. PMID:
25064009.



14. Goodkind M, Eickhoff SB, Oathes DJ, Jiang Y, Chang A, Jones-Hagata LB,
et al. Identification of a common neurobiological substrate for mental illness. JAMA Psychiatry 2015;72:305ŌĆō315. PMID:
25651064.



15. Sul JH, Han B, Ye C, Choi T, Eskin E. Effectively identifying eQTLs from multiple tissues by combining mixed model and meta-analytic approaches. PLoS Genet 2013;9:e1003491. PMID:
23785294.



16. Fisher RA. Statistical Methods for Research Workers. Edinburgh: Oliver and Boyd, 1925.
17. Han B, Eskin E. Random-effects model aimed at discovering associations in meta-analysis of genome-wide association studies. Am J Hum Genet 2011;88:586ŌĆō598. PMID:
21565292.



18. Fleiss JL. The statistical basis of meta-analysis. Stat Methods Med Res 1993;2:121ŌĆō145. PMID:
8261254.


19. Liptak T. On the combination of independent events. Magyar Tud Akad Mat Kutato Int Kozl 1958;3:171ŌĆō197.
20. Zaykin DV. Optimally weighted Z-test is a powerful method for combining probabilities in meta-analysis. J Evol Biol 2011;24:1836ŌĆō1841. PMID:
21605215.



21. Zhou B, Shi J, Whittemore AS. Optimal methods for meta-analysis of genome-wide association studies. Genet Epidemiol 2011;35:581ŌĆō591. PMID:
21922536.



22. Cochran WG. The combination of estimates from different experiments. Biometrics 1954;10:101ŌĆō129.

23. Mantel N, Haenszel W. Statistical aspects of the analysis of data from retrospective studies of disease. J Natl Cancer Inst 1959;22:719ŌĆō748. PMID:
13655060.

24. Won S, Morris N, Lu Q, Elston RC. Choosing an optimal method to combine P-values. Stat Med 2009;28:1537ŌĆō1553. PMID:
19266501.



25. Birch MW. The detection of partial association, I: the 2 ├Ś 2 case. J R Stat Soc Series B 1964;26:313ŌĆō324.

26. Pereira TV, Patsopoulos NA, Salanti G, Ioannidis JP. Discovery properties of genome-wide association signals from cumulatively combined data sets. Am J Epidemiol 2009;170:1197ŌĆō1206. PMID:
19808636.



27. Greene WH. Econometric Analysis. Harlow: Pearson Education, 2011.
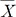 becomes
becomes 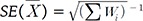 . The statistical significance can be tested by constructing a z-score statistic of IVW as follows, which asymptotically follows N(0,1) under the null hypothesis of no effects.
. The statistical significance can be tested by constructing a z-score statistic of IVW as follows, which asymptotically follows N(0,1) under the null hypothesis of no effects.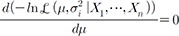 , we can obtain the maximum likelihood (ML) estimator: which is equivalent to the IVW statistic
, we can obtain the maximum likelihood (ML) estimator: which is equivalent to the IVW statistic 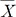 in equation (2). Therefore, the inverse variance-weighted average method is optimal in the sense that it maximizes the likelihood of observations with the optimized weight of Wi = (Žāi2)ŌłÆ1 [21,22].
in equation (2). Therefore, the inverse variance-weighted average method is optimal in the sense that it maximizes the likelihood of observations with the optimized weight of Wi = (Žāi2)ŌłÆ1 [21,22].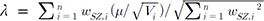 . Now, we want to obtain the weight wi that maximizes lambda. The optimal weight can be obtained by using the Cauchy-Schwarz inequality, as follows [12,21]:
. Now, we want to obtain the weight wi that maximizes lambda. The optimal weight can be obtained by using the Cauchy-Schwarz inequality, as follows [12,21]:
 and k are constants. Thus, the optimal weight is
and k are constants. Thus, the optimal weight is 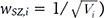 . Then, the resulting weighted SZ can be constructed as
. Then, the resulting weighted SZ can be constructed as
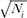 , because in many applications, the variance Vi is inversely proportional to the sample size Ni. However, we would like to note that in some applications, the variance can be a function of not only Ni but also other properties of the data. For example, in genetic association studies, when we test an association of a single-nucleotide polymorphism (SNP) to a phenotype, the variance is typically inversely proportional to Nipi(1ŌłÆpi), where pi denotes the allele frequency of the risk allele. This suggests that if the datasets that we want to combine have different allele frequencies, weighting the z-scores only by Ni can be suboptimal. Below, we will show by simulations that we can have some power loss by using just Ni as the weight, instead of accounting for frequency differences. However, the approximation of this weight
, because in many applications, the variance Vi is inversely proportional to the sample size Ni. However, we would like to note that in some applications, the variance can be a function of not only Ni but also other properties of the data. For example, in genetic association studies, when we test an association of a single-nucleotide polymorphism (SNP) to a phenotype, the variance is typically inversely proportional to Nipi(1ŌłÆpi), where pi denotes the allele frequency of the risk allele. This suggests that if the datasets that we want to combine have different allele frequencies, weighting the z-scores only by Ni can be suboptimal. Below, we will show by simulations that we can have some power loss by using just Ni as the weight, instead of accounting for frequency differences. However, the approximation of this weight 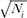 will be optimal when no heterogeneity can be found between the minor allele frequencies [2].
will be optimal when no heterogeneity can be found between the minor allele frequencies [2]. , which is assumed in Eq. (18). We assume that SZ uses SE(Xi)ŌłÆ1 as weights for z-scores, rather than only using sample sizes.
, which is assumed in Eq. (18). We assume that SZ uses SE(Xi)ŌłÆ1 as weights for z-scores, rather than only using sample sizes.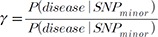 , ranging from 1.01 to 1.2. We assumed a meta-analysis of 5 genetic association studies and assumed a minor allele frequency (MAF) of 0.3. In an additional simulation setting, we assumed varying MAFs of (0.1,0.2,0.3,0.4,0.5) for the 5 studies. We assumed a very small disease prevalence (F Ōēł 0). Given these assumptions and parameters, we can calculate the expected MAF in cases and in controls. Specifically, given MAF p and relative risk ╬│, the case MAF becomes ╬│p/((╬│ŌłÆ1)p + 1), where the control MAF becomes approximately p, given F Ōēł 0. Given the expected MAF in cases and controls, we could randomly sample genotype data, assuming 500 cases and 500 controls for each of the five studies. To assess the statistical significance of the sample data, we used log odds ratio as a statistic, which follows an asymptotic normal distribution. We repeated the procedure to generate 100,000 simulated meta-analysis sets. Given the significance level ╬▒ = 0.05, the power was the proportion of sample sets whose meta-analysis p-value was Ōēż╬▒.
, ranging from 1.01 to 1.2. We assumed a meta-analysis of 5 genetic association studies and assumed a minor allele frequency (MAF) of 0.3. In an additional simulation setting, we assumed varying MAFs of (0.1,0.2,0.3,0.4,0.5) for the 5 studies. We assumed a very small disease prevalence (F Ōēł 0). Given these assumptions and parameters, we can calculate the expected MAF in cases and in controls. Specifically, given MAF p and relative risk ╬│, the case MAF becomes ╬│p/((╬│ŌłÆ1)p + 1), where the control MAF becomes approximately p, given F Ōēł 0. Given the expected MAF in cases and controls, we could randomly sample genotype data, assuming 500 cases and 500 controls for each of the five studies. To assess the statistical significance of the sample data, we used log odds ratio as a statistic, which follows an asymptotic normal distribution. We repeated the procedure to generate 100,000 simulated meta-analysis sets. Given the significance level ╬▒ = 0.05, the power was the proportion of sample sets whose meta-analysis p-value was Ōēż╬▒. is broken. We have already shown that a MAF difference can result in such breakage of this relationship. Here, additionally, we show that the use of a linear mixed model can also result in such breakage of the relationship
is broken. We have already shown that a MAF difference can result in such breakage of this relationship. Here, additionally, we show that the use of a linear mixed model can also result in such breakage of the relationship  . We used the data of the Wellcome Trust Case Control Consortium [28]. This dataset includes approximately 2,000 cases for each of seven different diseases and 1,500 controls for each of two control groups (1958C and National Bureau of Standards [NBS]). We used the data on rheumatoid arthritis (RA) and type 1 diabetes (T1D). After standard quality-control and removal of the MHC region, we obtained 469,225 SNPs. We performed association tests for two diseases; we performed association tests for RA using NBS as controls and association tests for T1D using 1958C as controls. The sample sizes for the two association tests were similar (N = 3,318 and 3,443, respectively). We used logistic regression implemented in plink (with--logistic command). Because the sample sizes of the two tests were similar, we expected that for each SNP, the standard errors of the effect size estimate would be similar. That is, we wanted to test if the relationship
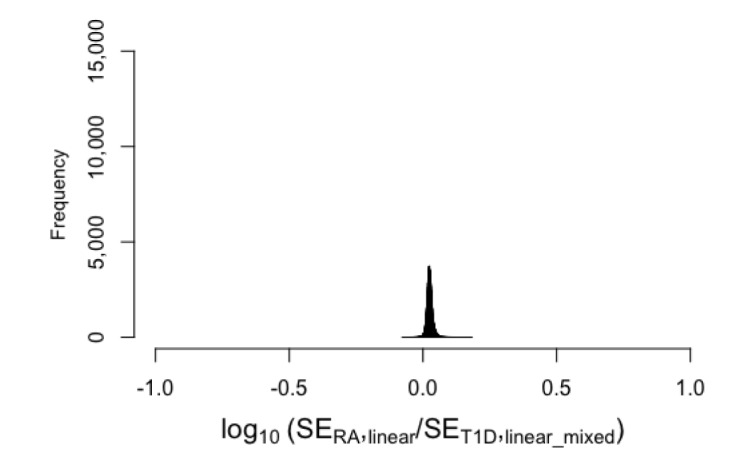
. We used the data of the Wellcome Trust Case Control Consortium [28]. This dataset includes approximately 2,000 cases for each of seven different diseases and 1,500 controls for each of two control groups (1958C and National Bureau of Standards [NBS]). We used the data on rheumatoid arthritis (RA) and type 1 diabetes (T1D). After standard quality-control and removal of the MHC region, we obtained 469,225 SNPs. We performed association tests for two diseases; we performed association tests for RA using NBS as controls and association tests for T1D using 1958C as controls. The sample sizes for the two association tests were similar (N = 3,318 and 3,443, respectively). We used logistic regression implemented in plink (with--logistic command). Because the sample sizes of the two tests were similar, we expected that for each SNP, the standard errors of the effect size estimate would be similar. That is, we wanted to test if the relationship  held well for these real data. Fig. 2A shows that when we plotted the log10 value of the ratio of the two standard errors, the values were highly concentrated around 0. This implies that the standard errors were very similar between RA and T1D, as expected, because the sample sizes were similar. Thus, the relationship
held well for these real data. Fig. 2A shows that when we plotted the log10 value of the ratio of the two standard errors, the values were highly concentrated around 0. This implies that the standard errors were very similar between RA and T1D, as expected, because the sample sizes were similar. Thus, the relationship  approximately held well. Therefore, Fig. 2A shows that IVW and SZ_N have similar results in this situation.
approximately held well. Therefore, Fig. 2A shows that IVW and SZ_N have similar results in this situation. does not hold. As a result, in the meta-analysis, the p-values of IVW and SZ_N differed dramatically. Note that the standard errors given by GEMMA can be slightly different from the standard linear model, because GEMMA regresses the effect of population structure. However, an additional analysis comparing the standard errors of GEMMA and the standard linear model demonstrated that this effect is minimal and that their standard errors were similar (Fig. 3). Thus, the difference observed between GEMMA and the logistic regression model was mainly due to the use of different models (linear and logistic).
does not hold. As a result, in the meta-analysis, the p-values of IVW and SZ_N differed dramatically. Note that the standard errors given by GEMMA can be slightly different from the standard linear model, because GEMMA regresses the effect of population structure. However, an additional analysis comparing the standard errors of GEMMA and the standard linear model demonstrated that this effect is minimal and that their standard errors were similar (Fig. 3). Thus, the difference observed between GEMMA and the logistic regression model was mainly due to the use of different models (linear and logistic).