Risk Prediction Using Genome-Wide Association Studies on Type 2 Diabetes

Article information

Genomics Inform. 2016;14(4):138-148

Publication date (electronic) : 2016 December 30

doi : https://doi.org/10.5808/GI.2016.14.4.138

Sungkyoung Choi ¹, Sunghwan Bae ¹, Taesung Park ¹^,²

¹Interdisciplinary Program in Bioinformatics, Seoul National University, Seoul 08826, Korea.

²Department of Statistics, Seoul National University, Seoul 08826, Korea.

Corresponding author: Tel: +82-2-880-8924, Fax: +82-2-883-6144, tspark@stats.snu.ac.kr

Received 2016 November 10; Revised 2016 December 05; Accepted 2016 December 05.

Abstract

The success of genome-wide association studies (GWASs) has enabled us to improve risk assessment and provide novel genetic variants for diagnosis, prevention, and treatment. However, most variants discovered by GWASs have been reported to have very small effect sizes on complex human diseases, which has been a big hurdle in building risk prediction models. Recently, many statistical approaches based on penalized regression have been developed to solve the “large p and small n” problem. In this report, we evaluated the performance of several statistical methods for predicting a binary trait: stepwise logistic regression (SLR), least absolute shrinkage and selection operator (LASSO), and Elastic-Net (EN). We first built a prediction model by combining variable selection and prediction methods for type 2 diabetes using Affymetrix Genome-Wide Human SNP Array 5.0 from the Korean Association Resource project. We assessed the risk prediction performance using area under the receiver operating characteristic curve (AUC) for the internal and external validation datasets. In the internal validation, SLR-LASSO and SLR-EN tended to yield more accurate predictions than other combinations. During the external validation, the SLR-SLR and SLR-EN combinations achieved the highest AUC of 0.726. We propose these combinations as a potentially powerful risk prediction model for type 2 diabetes.

Keywords: clinical prediction rule; genome-wide association study; penalized regression models; type 2 diabetes mellitus

Introduction

Genome-wide association studies (GWASs) have successfully identified susceptibility variants associated with human diseases. However, most susceptibility variants have small effect sizes and explain only a small proportion of heritability [1]. The presence of a large number of variants genotyped for a small number of subjects (commonly known as “large p small n”) has been one major challenge in building disease risk prediction models. Furthermore, the issue of multicollinearity arises when there is high linkage disequilibrium (LD) among single-nucleotide polymorphisms (SNPs). Multiple regression is very unstable and sensitive due to multicollinearity, in which the coefficient estimates have very large variances [2]. Recently, various statistical approaches have been proposed to cope with these issues.

Traditional approaches for disease risk prediction have been based on gene scores (GSs) [3 4 5 6]. The marginal effects of previously known disease-associated loci are estimated, and then, their sum can be used to construct a risk prediction model. While GS-based approaches can be useful when a genetic variant is responsible for diseases [7], they show low prediction performance when multiple genetic variants exist for a complex disease [8 9]. For example, the prediction performance for coronary heart and disease type 2 diabetes (T2D) is only 0.59 and 0.58, respectively, for area under the receiver operating characteristic curve (AUC) values [8 9].

For complex diseases, a more accurate and reliable prediction model is required. Multiple logistic regression (MLR) is a classification method that utilizes combined information across multiple genetic variants. Several studies have shown that the MLR-based approach is useful in building a disease risk prediction model [10 11 12 13]. However, if there is large LD between SNPs, the parameter estimates of MLR become unstable, and as a result, the risk prediction model has weak predictive power.

As an alternative to MLR, data mining approaches have been used widely to improve risk prediction performance. In particular, support vector machine (SVM) [14 15] and random forest [16 17] have been shown to outperform other classification algorithms [18]. Although these data mining approaches may provide very useful tools in classification, the effects of genetic variants on a disease in prediction models are not easy to interpret. Furthermore, these approaches do not give class conditional probabilities of individual predictions [19]. Thus, we focus mainly on penalized regression approaches in this paper, which provides an individual prediction result in terms of probability.

As mentioned before, the problem of “large p small n” interrupts the estimation of the joint effect of multiple genetic variants. In order to overcome this, various penalized regression approaches have been proposed, such as ridge [20 21 22], least absolute shrinkage and selection operator (LASSO) [23], and Elastic-Net (EN) [24]. These penalized approaches have an advantage in terms of both variable selection and prediction power over non-penalized approaches for high-dimensional data. For instance, the prediction performance for Crohn disease and inflammatory bowel disease using a number of genetic variants with penalized approaches has been shown to improve [25 26].

In this study, we investigated the effect of variable selection on the performance of prediction methods. Especially, we considered the following methods for variable selection and prediction: stepwise logistic regression (SLR), LASSO, and EN. We compared the effect of variable selection on the performance of prediction by applying them to T2D GWAS chip data. We constructed the prediction models by combining variable selection and prediction methods using the Korean Association Resource (KARE) GWAS dataset (3,180 individuals) and then evaluated the performance of the risk prediction model through both internal validation (805 individuals in the KARE testing dataset) and external validation (4,723 individuals in an external replication dataset). The external replication dataset combined two cohorts: the Health2 study (1,816 individuals) and Health Examinee (HEXA) study (3,696 individuals). In both the internal and external validation datasets, we measured the discriminative accuracy of the prediction models using AUC.

Methods

KARE dataset

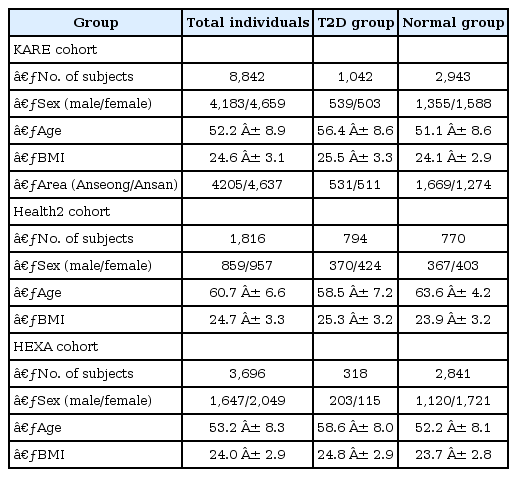
The KARE project was initiated in 2007 to undertake a large-scale GWAS with 10,038 participants from two community-based cohorts (i.e., the rural Anseong and urban Ansan cohorts). Among the participants, 10,004 samples were genotyped using Affymetrix Genome-Wide Human SNP Array 5.0 Affymetrix, Santa Clara, CA, USA). From sample and SNP quality controls, a total of 8,842 individuals were selected from the Anseong (2,374 men and 2,263 women) and Ansan (1,809 men and 2,396 women) cohorts [27]. Missing genotypes were imputed using the Beale software program [28].

In this study, a total of 3,985 samples were selected from among the 8,842 individuals using T2D diagnostic criteria [29 30]. A total of 1,042 subjects were included in the T2D group according to the following criteria: (1) fasting plasma glucose (FPG) larger than or equal to 126 mg/dL, 2-hour postprandial blood glucose (Glu120) larger than or equal to 200 mg/dL, (2) treatment of T2D, and (3) age of disease onset ≥ 40 years. The inclusion criteria for nondiabetic normal subjects (n = 2,943) were as follows: (1) FPG less than or equal to 100 mg/dL or Glu120 less than or equal to 140 mg/dL and (2) no history of diabetes. The demographic variables of the subjects are summarized in Table 1.

Table 1.

Demographic variables for KARE, Health2, and HEXA cohorts

Health2 and HEXA datasets

We combined two Korean GWASs, the Health2 study (n = 1,816) and the HEXA study (n = 3,696). The Health2 study consists of community-based cohorts from 5 rural areas (i.e., Wonju, Pyeongchang, Gangneung, Geumsan, and Naju), and the HEXA study is a cohort from 14 urban areas. These samples were genotyped using the Affymetrix Genome-Wide Human SNP array 6.0. The Health2 and the HEXA cohorts have been described in previous studies [27 31 32]. Missing genotypes were were imputed using Beagle software.

Our investigation was based on the analysis of an external replication dataset of 4,723 samples (1,112 T2D subjects, 3,611 normal subjects) for T2D [33]. The criteria for grouping T2D subjects (n_Health2 = 794, n_HEXA = 318) and nondiabetic normal subjects (n_Health2 = 770, n_HEXA = 2,841) were FPG level (FPG ≥ 126 for T2D subjects and FPG ≤ 100 for nondiabetic normal subjects) and history of T2D treatment. The demographic variables of the subjects in the Health2 and HEXA cohorts are summarized in Table 1.

Statistical analysis

For the joint identification of disease susceptibility variants among a large number of SNPs, we extracted SNPs having a strong correlation with T2D via logistic regression for single-variant analysis and collected the list of reported SNPs from a GWAS catalog [34]. Then, we implemented a 3-stage procedure as follows: the first stage was variable selection using SLR, LASSO, and EN. The second stage was the construction of risk prediction models. The third stage was evaluation of the risk prediction models through both internal validation and external validation.

SNP sets

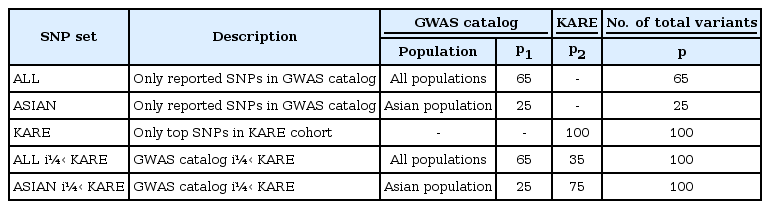
Because the components of SNPs seem to be related to the performance of risk prediction, we used two data sources (i.e., the GWAS catalog and KARE cohort). First, we collected the SNPs, p₁, from a GWAS catalog in all populations and an Asian population only. Second, the SNPs were selected by single-variant association test using logistic regression, with adjustments for age, sex, area (namely, rural area of Anseong and urban area of Ansan), and body mass index (BMI). We chose the top-ranked p₂ SNPs by the order of p-values from the KARE cohort. In Table 2, we have categorized five SNP sets.

Table 2.

List of the SNP sets

(1) ALL (SNPs only reported in the GWAS catalog)
(2) ASIAN (SNPs only reported in the GWAS catalog with an Asian population)
(3) KARE (only top-ranked p₂ SNPs in the KARE cohort)
(4) ALL + KARE (combined SNPs in the GWAS catalog and KARE cohort)
(5) ASIAN + KARE (combined SNPs in the GWAS catalog with an Asian population and the KARE cohort)

Stage 1: Variable selection

In the KARE dataset, we separated 3,985 individuals (1,042 T2D subjects, 2,943 normal subjects) into a training set of 3,180 individuals (830 T2D subjects, 2,350 normal subjects) and a test set of 805 individuals (212 T2D subjects, 593 normal subjects) (see Fig. 1). The variable selection was performed using 5-fold cross-validation (CV) on the training set. We describe the details below.

Fig. 1

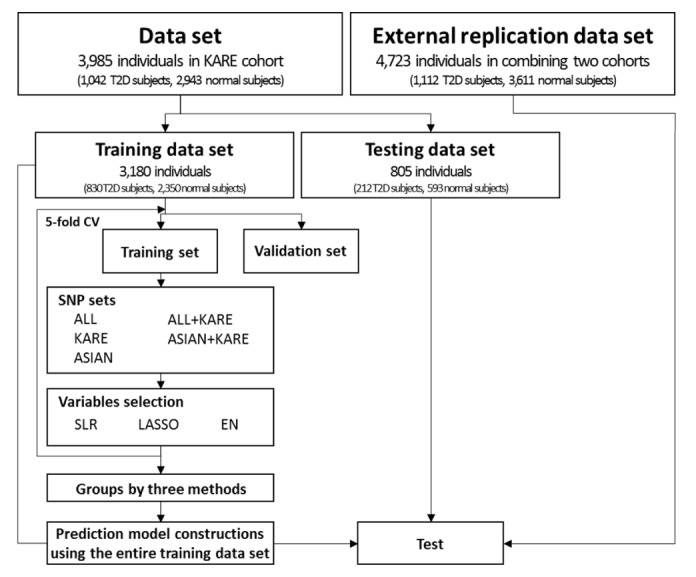
Outline of the risk prediction model construction and validation. T2D, type 2 diabetes; CV, cross-validation; ALL, single-nucleotide polymorphisms (SNPs) only reported in the genome-wide association study (GWAS) catalog; KARE, Korean Association Resource; ASIAN, SNPs only reported in the GWAS catalog with an Asian population; ALL + KARE, combined SNPs in the GWAS catalog and KARE cohort; ASIAN + KARE, combined SNPs in the GWAS catalog with an Asian population and the KARE cohort; SLR, stepwise logistic regression; LASSO, least absolute shrinkage and selection operator; EN, Elastic-Net.

The phenotype y_i of subject i = 1, …, n was set as a dependent variable (T2D = 1, normal = 0), and the genotype x_ij of the j-th SNP (j = 1, …, p) for subject i was set as an independent variable with an additive genetic model (AA = 0, Aa = 1, aa=2, where A and a indicate the major and minor alleles, respectively).

For variable selection, the following SLR was conducted.

logP(yi=1)1−P(yi=1)=β0+∑j=1pβjxij+γ1AGEi+γ2SEXi+γ3AREAi+γ4BMIi

where β₀ and β_j are the intercept and effect sizes of SNPs, respectively. γ₁, γ₂, γ₃, and γ₄ represent the age, sex, area (namely, rural and urban areas), and BMI of the i-th individuals, respectively. For the given covariates, the selection of SNPs was determined by a stepwise procedure based on Akaike’s information criterion [35]. The stepwise procedure was conducted using the R-package MASS [36].

The penalized method solves the following:

minβ0, β, γ∑i=1n(yi−β0−X′iβ−COV′iγ)2+Pλ(β)

where X_i = (x_i1, …, x_ij, …, x_ip)^T and COV_i = (AGE_i, SEX_i, AREA_i, BMI_i)^T for the i-th subject, β = (β₁, …, β_j, …, β_p)^T, and γ = (γ₁, γ₂, γ₃, γ₄)^T. Lasso and EN penalties are defined as P_λ(β) = λΣ|β| and P_λ(β) = λ[(1 − α)Σ|β| + αΣβ²], respectively. λ and α are a tuning parameter and a weight of a value between 0 to 1, respectively. All penalized methods were conducted using the R-package glmnet [37].

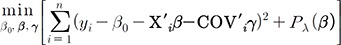Then, we defined five sets as follows:

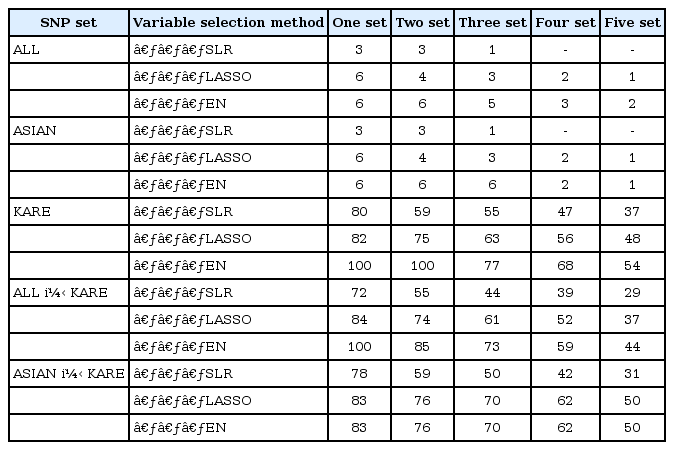
(1) One set: set of SNPs that have a non-zero coefficient at least one time among the 5-fold CV
(2) Two set: set of SNPs that have a non-zero coefficient at least two times among the 5-fold CV
(3) Three set: set of SNPs that have a non-zero coefficient at least three times among the 5-fold CV
(4) Four set: set of SNPs that have a non-zero coefficient at least four times among the 5-fold CV
(5) Five set: set of SNPs having non-zero coefficients in the 5-fold CV,

where one set ⊃ two set ⊃ three set ⊃ four set ⊃ five set.

Stage 2: Construction of risk prediction models

For construction of the risk prediction model, we considered 9 combinations of variable selection and prediction methods (i.e., SLR-SLR, SLR-LASSO, SLR-EN, LASSO-SLR, LASSO-LASSO, LASSO-EN, EN-SLR, EN-LASSO, and EN-EN). For each combination, we constructed prediction models using the entire KARE training dataset (n = 3,180).

Stage 3: Evaluation of risk prediction models

For evaluating the risk prediction performance, we needed to assess both internally and externally to determine the performance of the prediction models. To validate the risk prediction methods, we used internal and external validation datasets from the KARE testing dataset (n = 805) and an external replication dataset (n = 4,723), respectively. In both the internal and external validation datasets, we used the AUC of the receiver operator characteristic (ROC) curve, which is widely used for risk prediction performance [38 39]. The ROC curve is a graphical plot of sensitivity (true positive rate) against 1 – specificity (false-positive rate) across all possible threshold values. A summary measure of ROC curves, such as AUC, is indicated as the discriminative accuracy. An AUC score close to 0.5 reflects random chance, while AUC values closer to 1 indicate perfect accuracy.

Results

Preparing SNP sets

The association of T2D was analyzed using logistic regression with adjustments for age, sex, area, and BMI as covariates. As shown in Supplementary Fig. 1A, the quantile-quantile plot shows that the observed p -values at the tail are significantly larger than the null distribution. Six SNPs in CDKAL1 had associations that reached a genome-wide significance level of p-value less than 1.45 × 10⁻⁷ (Supplementary Table 1, Supplementary Fig. 1B). Supplementary Table 1 shows the results with a p-value threshold of less than 5.00 × 10⁻⁵. rs7754840 (p = 4.66 × 10⁻⁸) of CDKAL1 and rs10811661 (p = 7.17 × 10⁻⁶) of CDKN2A/2B have been observed to affect T2D in previous GWASs [40 41 42 43 44 45]. In the GWAS catalog, we found 65 SNPs and 25 SNPs associated with T2D in all populations and the Asian population, respectively (Supplementary Table 2). As previously mentioned, we categorized five SNP sets from two data sources in Table 2.

Selection of predictor variables

In each SNP set, the variable selection methods were applied to 5-fold CV on the training set. Fig. 2 shows information about the number of overlapping SNPs by 5-fold CV for each variable selection method. Table 3 provides a summary of the results of the variable selection. The variable selection methods gave very similar results in the ALL and ASIAN datasets, whereas the results showed differences among the methods in the KARE and ALL + KARE datasets. Furthermore, SLR generally tended to select a smaller number of SNPs than LASSO and EN.

Fig. 2

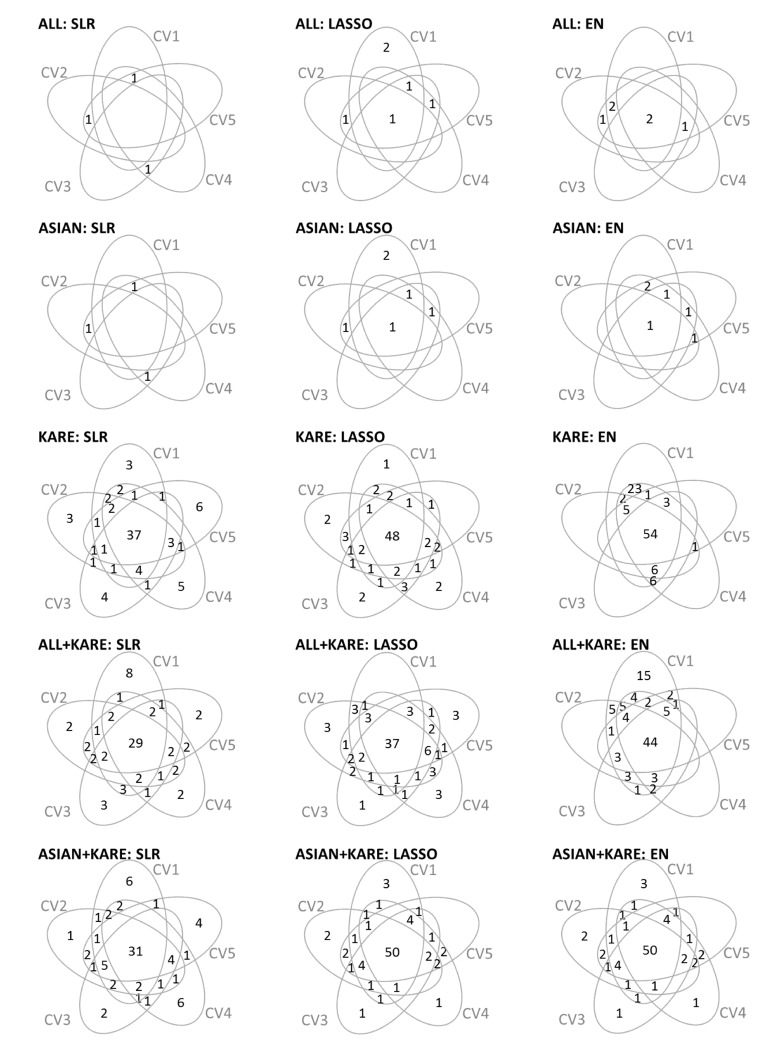
Venn diagrams summarizing the number of variables shared among 5-fold CV by variables selection methods. CV, cross-validation; ALL, single-nucleotide polymorphisms (SNPs) only reported in the genome-wide association study (GWAS) catalog; ASIAN, SNPs only reported in the GWAS catalog with an Asian population; KARE, Korean Association Resource; ALL + KARE, combined SNPs in the GWAS catalog and KARE cohort; ASIAN + KARE, combined SNPs in the GWAS catalog with an Asian population and the KARE cohort; SLR, stepwise logistic regression; LASSO, least absolute shrinkage and selection operator; EN, Elastic-Net.

Table 3.

Number of overlapping SNPs selected by 5-fold CV for each variable selection method

Construction of prediction models and validation in testing datasets

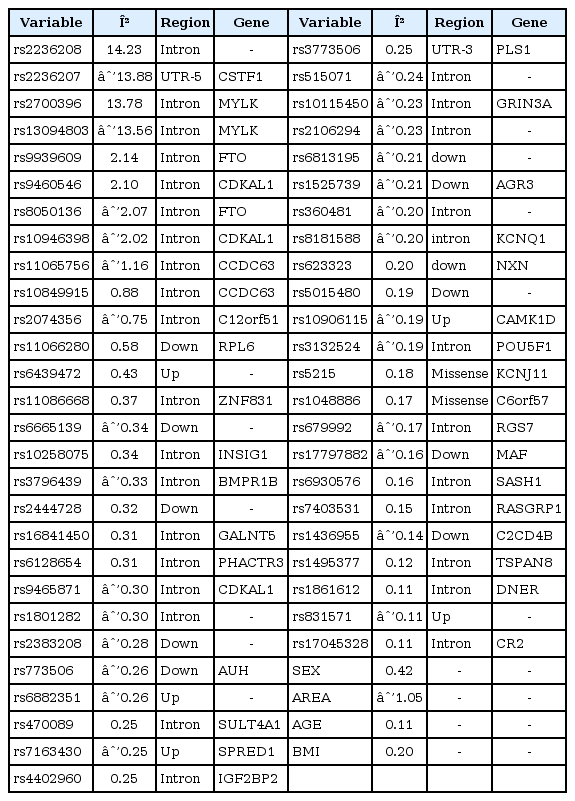
We fitted the prediction models using SLR, LASSO, and EN using the entire training individuals in the KARE cohort. Then, we applied the prediction models to the KARE testing dataset and an external replication dataset. The prediction models were built based on Affymetrix 5.0, but the external replication dataset was generated by Affymetrix 6.0. In the case of the KARE dataset, nearly 90% of the SNPs belonged to the external replication dataset. Thus, we did not include untyped SNPs in the evaluation of prediction models using the replication dataset. Among the five SNP sets, Fig. 3 shows that the prediction models from the KARE SNP set had higher AUC values for the KARE testing dataset than other SNP sets. In contrast, as shown in Fig. 4, the prediction models from ALL + KARE had the best performance overall for the external replication dataset. In Table 4, the best combinations of the variable selection and prediction models had the highest AUC values. SLR-LASSO and SLR-EN with three set from KARE had an AUC of 0.816 in the KARE testing dataset. In an external replication dataset, SLR-SLR and SLR-EN with one set from ALL + KARE (AUC, 0.726) were the best, with 51 SNPs for T2D, while SLR-LASSO and SLR-EN with three set from KARE (AUC, 0.590) showed the best performance, with 53 SNPs. SLR-SLR with one set from ALL + KARE was superior to the model with only demographic variables (15.7% increase in AUC). Among the 51 SNPs of SLR-SLR with one set from ALL + KARE, 38 SNPs were mapped to the genes (Table 5). Some genes (AGR3, C2CD4B, C6orf57, CAMK1D, DNER, IGF2BP2, KCNJ11, KCNQ1, NXN, PLS1, and RGS7) were previously reported to be associated with T2D [44 45 46 47 48 49 50 51 52 53].

Fig. 3

Internal validation shows the AUC values for each combination of variable selection and prediction methods. Each bar represents one of five SNP data sets. AUC, area under the receiver operating characteristic curve; SNP, single-nucleotide polymorphism; ALL, SNPs only reported in the genome-wide association study (GWAS) catalog; ASIAN, SNPs only reported in the GWAS catalog with an Asian population; KARE, Korean Association Resource; ALL + KARE, combined SNPs in the GWAS catalog and KARE cohort; ASIAN + KARE, combined SNPs in the GWAS catalog with an Asian population and the KARE cohort; SLR, stepwise logistic regression; LASSO, least absolute shrinkage and selection operator; EN, Elastic-Net.

Fig. 4

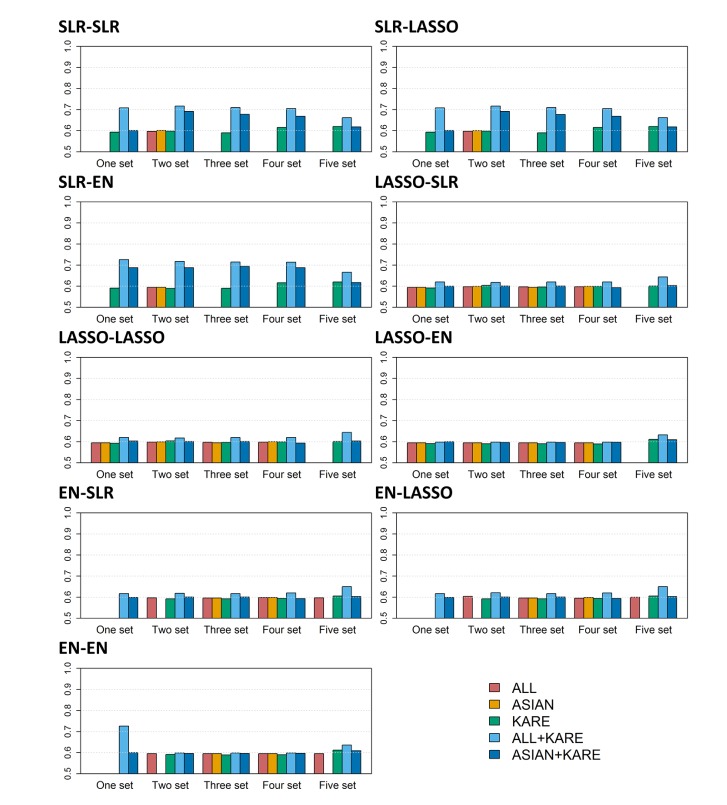
External validation shows the AUC values for each combination of variable selection and prediction methods. Each bar represents one of five SNP data sets. AUC, area under the receiver operating characteristic curve; SNP, single-nucleotide polymorphism; ALL, SNPs only reported in the genome-wide association study (GWAS) catalog; ASIAN, SNPs only reported in the GWAS catalog with an Asian population; KARE, Korean Association Resource; ALL + KARE, combined SNPs in the GWAS catalog and KARE cohort; ASIAN + KARE, combined SNPs in the GWAS catalog with an Asian population and the KARE cohort; SLR, stepwise logistic regression; LASSO, least absolute shrinkage and selection operator; EN, Elastic-Net.

Table 4.

Summary of prediction performance in KARE testing dataset and an external replication dataset

Table 5.

Development of SLR-SLR prediction model with one set from ALL + KARE for predicting T2D

Discussion

In this study, we compared the performance of risk prediction models combining variable selection and prediction methods. Also, the effect of five SNP sets (i.e., ALL, ASIAN, KARE, ALL + KARE, and ASIAN + KARE) on risk prediction performance was investigated. Overall, we confirmed that prediction models incorporating both demographic variables and genetic variables were more accurate than prediction models using only demographic variables. According to our results, the best combinations were SLR-LASSO and SLR-EN with three set from the KARE SNP set in the KARE testing dataset, whereas the SLR-SLR and SLR-EN combination with one set from the ALL + KARE SNP set outperformed all other combinations in an external replication dataset.

The analysis of risk prediction studies can be extended in several ways. First, the performance of a risk prediction model can be improved by incorporating rare variants. Advances in sequencing technology make it possible to investigate the role of common and rare variants in risk prediction of complex diseases. Wei and Lu [54] proposed a collapsing ROC approach that incorporates genetic information from both common and rare variants. A prediction algorithm based on SVM with common and rare variants was proposed in order to improve predictive performance [55]. Second, integrating biological knowledge into a risk prediction model will provide more accurate predictions and biologically meaningful interpretation. Eleftherohorinou et al. [56] have shown success of a pathway-based prediction test of GWAS data. Recently, a pathway-based approach was proposed to incorporate principal components of pathway effects and pathway-covariate interactions into logistic regression [57]. Furthermore, a risk prediction model can be used to investigate multiple types of omics data, such as The Cancer Genome Atlas datasets. The recent developments of single-molecule sequencing technologies (i.e., third-generation sequencing) has facilitated integrated analysis of multi-omics data. There is no doubt that multi-omics data will lead to improvement of risk prediction models.

Acknowledgments

This research was supported by a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (HI15C2165), and the Bio-Synergy Research Project (2013M3A9C4078158) of the Ministry of Science, ICT and Future Planning through the National Research Foundation. The GWAS chip data were supported by bioresources from the National Biobank of Korea, the Centers for Disease Control and Prevention, Republic of Korea (4845-301, 4851-302 and -307).

References

1. Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, et al. Finding the missing heritability of complex diseases. Nature 2009;461:747–753. 19812666.

2. Wang WY, Barratt BJ, Clayton DG, Todd JA. Genome-wide association studies: theoretical and practical concerns. Nat Rev Genet 2005;6:109–118. 15716907.

3. Evans DM, Visscher PM, Wray NR. Harnessing the information contained within genome-wide association studies to improve individual prediction of complex disease risk. Hum Mol Genet 2009;18:3525–3531. 19553258.

4. International Schizophrenia Consortium. Purcell SM, Wray NR, Stone JL, Visscher PM, O’Donovan MC, et al. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature 2009;460:748–752. 19571811.

5. Davies RW, Dandona S, Stewart AF, Chen L, Ellis SG, Tang WH, et al. Improved prediction of cardiovascular disease based on a panel of single nucleotide polymorphisms identified through genome-wide association studies. Circ Cardiovasc Genet 2010;3:468–474. 20729558.

6. Hughes MF, Saarela O, Stritzke J, Kee F, Silander K, Klopp N, et al. Genetic markers enhance coronary risk prediction in men: the MORGAM prospective cohorts. PLoS One 2012;7:e40922. 22848412.

7. Janssens AC, van Duijn CM. Genome-based prediction of common diseases: advances and prospects. Hum Mol Genet 2008;17:R166–R173. 18852206.

8. van der Net JB, Janssens AC, Sijbrands EJ, Steyerberg EW. Value of genetic profiling for the prediction of coronary heart disease. Am Heart J 2009;158:105–110. 19540399.

9. Weedon MN, McCarthy MI, Hitman G, Walker M, Groves CJ, Zeggini E, et al. Combining information from common type 2 diabetes risk polymorphisms improves disease prediction. PLoS Med 2006;3:e374. 17020404.

10. Wacholder S, Hartge P, Prentice R, Garcia-Closas M, Feigelson HS, Diver WR, et al. Performance of common genetic variants in breast-cancer risk models. N Engl J Med 2010;362:986–993. 20237344.

11. Jostins L, Barrett JC. Genetic risk prediction in complex disease. Hum Mol Genet 2011;20:R182–R188. 21873261.

12. Lindström S, Schumacher FR, Cox D, Travis RC, Albanes D, Allen NE, et al. Common genetic variants in prostate cancer risk prediction--results from the NCI Breast and Prostate Cancer Cohort Consortium (BPC3). Cancer Epidemiol Biomarkers Prev 2012;21:437–444. 22237985.

13. Kundu S, Mihaescu R, Meijer CM, Bakker R, Janssens AC. Estimating the predictive ability of genetic risk models in simulated data based on published results from genome-wide association studies. Front Genet 2014;5:179. 24982668.

14. Cortes C, Vapnik V. Support-vector networks. Mach Learn 1995;20:273–297.

15. Burges CJ. A tutorial on support vector machines for pattern recognition. Data Min Knowl Discov 1998;2:121–167.

16. Breiman L. Random forests. Mach Learn 2001;45:5–32.

17. Banfield RE, Hall LO, Bowyer KW, Kegelmeyer WP. A comparison of decision tree ensemble creation techniques. IEEE Trans Pattern Anal Mach Intell 2007;29:173–180. 17108393.

18. Yoon D, Kim YJ, Park T. Phenotype prediction from genome-wide association studies: application to smoking behaviors. BMC Syst Biol 2012;6(Suppl 2):S11.

19. John Lu ZQ. The elements of statistical learning: data mining, inference, and prediction. J R Stat Soc Ser A Stat Soc 2010;173:693–694.

20. Hoerl AE. Ridge regression. Biometrics 1970;26:603.

21. Hoerl AE, Kennard RW. Ridge regression: applications to nonorthogonal problems. Technometrics 1970;12:69–82.

22. Hoerl AE, Kennard RW. Ridge regression: biased estimation for nonorthogonal problems. Technometrics 1970;12:55–67.

23. Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc Ser B Methodol 1996;58:267–288.

24. Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc Ser B Stat Methodol 2005;67:301–320.

25. Kooperberg C, LeBlanc M, Obenchain V. Risk prediction using genome-wide association studies. Genet Epidemiol 2010;34:643–652. 20842684.

26. Wei Z, Wang W, Bradfield J, Li J, Cardinale C, Frackelton E, et al. Large sample size, wide variant spectrum, and advanced machine-learning technique boost risk prediction for inflammatory bowel disease. Am J Hum Genet 2013;92:1008–1012. 23731541.

27. Cho YS, Go MJ, Kim YJ, Heo JY, Oh JH, Ban HJ, et al. A large-scale genome-wide association study of Asian populations uncovers genetic factors influencing eight quantitative traits. Nat Genet 2009;41:527–534. 19396169.

28. Browning SR, Browning BL. Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering. Am J Hum Genet 2007;81:1084–1097. 17924348.

29. Cho YS, Chen CH, Hu C, Long J, Ong RT, Sim X, et al. Meta-analysis of genome-wide association studies identifies eight new loci for type 2 diabetes in east Asians. Nat Genet 2011;44:67–72. 22158537.

30. Go MJ, Hwang JY, Park TJ, Kim YJ, Oh JH, Kim YJ, et al. Genome-wide association study identifies two novel loci with sex-specific effects for type 2 diabetes mellitus and glycemic traits in a Korean population. Diabetes Metab J 2014;38:375–387. 25349825.

31. Health Examinees Study Group. The Health Examinees (HEXA) study: rationale, study design and baseline characteristics. Asian Pac J Cancer Prev 2015;16:1591–1597. 25743837.

32. Wen W, Kato N, Hwang JY, Guo X, Tabara Y, Li H, et al. Genome-wide association studies in East Asians identify new loci for waist-hip ratio and waist circumference. Sci Rep 2016;6:17958. 26785701.

33. Lim J, Koh I, Cho YS. Identification of genetic loci stratified by diabetic status and microRNA related SNPs influencing kidney function in Korean populations. Genes Genom 2016;38:601–609.

34. Welter D, MacArthur J, Morales J, Burdett T, Hall P, Junkins H, et al. The NHGRI GWAS Catalog, a curated resource of SNP-trait associations. Nucleic Acids Res 2014;42:D1001–D1006. 24316577.

35. Akaike H. A new look at the statistical model identification. IEEE Trans Automat Contr 1974;19:716–723.

36. Ripley B, Venables B, Bates DM, Hornik K, Gebhardt A, Firth D, et al. Package ‘MASS’ CRAN Repository; 2013. Accessed 2016 Nov 1. Available from: http://cran r-project org/web/packages/MASS/MASS pdf.

37. Friedman J, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J Stat Softw 2010;33:1–22. 20808728.

38. DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 1988;44:837–845. 3203132.

39. Lasko TA, Bhagwat JG, Zou KH, Ohno-Machado L. The use of receiver operating characteristic curves in biomedical informatics. J Biomed Inform 2005;38:404–415. 16198999.

40. Diabetes Genetics Initiative of Broad Institute of Harvard and MIT. Lund University. Novartis Institutes of BioMedical Research. Saxena R, Voight BF, Lyssenko V, Burtt NP, de Bakker PI, et al. Genome-wide association analysis identifies loci for type 2 diabetes and triglyceride levels. Science 2007;316:1331–1336. 17463246.

41. Zeggini E, Weedon MN, Lindgren CM, Frayling TM, Elliott KS, Lango H, et al. Replication of genome-wide association signals in UK samples reveals risk loci for type 2 diabetes. Science 2007;316:1336–1341. 17463249.

42. Scott LJ, Mohlke KL, Bonnycastle LL, Willer CJ, Li Y, Duren WL, et al. A genome-wide association study of type 2 diabetes in Finns detects multiple susceptibility variants. Science 2007;316:1341–1345. 17463248.

43. Kwak SH, Kim SH, Cho YM, Go MJ, Cho YS, Choi SH, et al. A genome-wide association study of gestational diabetes mellitus in Korean women. Diabetes 2012;61:531–541. 22233651.

44. DIAbetes Genetics Replication And Meta-analysis (DIAGRAM) Consortium. Asian Genetic Epidemiology Network Type 2 Diabetes (AGEN-T2D) Consortium. South Asian Type 2 Diabetes (SAT2D) Consortium. Mexican American Type 2 Diabetes (MAT2D) Consortium. Type 2 Diabetes Genetic Exploration by Nex-generation sequencing in muylti-Ethnic Samples (T2D-GENES) Consortium. Mahajan A, et al. Genome-wide trans-ancestry meta-analysis provides insight into the genetic architecture of type 2 diabetes susceptibility. Nat Genet 2014;46:234–244. 24509480.

45. Hara K, Fujita H, Johnson TA, Yamauchi T, Yasuda K, Horikoshi M, et al. Genome-wide association study identifies three novel loci for type 2 diabetes. Hum Mol Genet 2014;23:239–246. 23945395.

46. Pasquale LR, Loomis SJ, Aschard H, Kang JH, Cornelis MC, Qi L, et al. Exploring genome-wide - dietary heme iron intake interactions and the risk of type 2 diabetes. Front Genet 2013;4:7. 23386860.

47. Sim X, Ong RT, Suo C, Tay WT, Liu J, Ng DP, et al. Transferability of type 2 diabetes implicated loci in multi-ethnic cohorts from Southeast Asia. PLoS Genet 2011;7:e1001363. 21490949.

48. Hanson RL, Muller YL, Kobes S, Guo T, Bian L, Ossowski V, et al. A genome-wide association study in American Indians implicates DNER as a susceptibility locus for type 2 diabetes. Diabetes 2014;63:369–376. 24101674.

49. Anderson D, Cordell HJ, Fakiola M, Francis RW, Syn G, Scaman ES, et al. First genome-wide association study in an Australian aboriginal population provides insights into genetic risk factors for body mass index and type 2 diabetes. PLoS One 2015;10:e0119333. 25760438.

50. Timpson NJ, Lindgren CM, Weedon MN, Randall J, Ouwehand WH, Strachan DP, et al. Adiposity-related heterogeneity in patterns of type 2 diabetes susceptibility observed in genome-wide association data. Diabetes 2009;58:505–510. 19056611.

51. Ng MC, Shriner D, Chen BH, Li J, Chen WM, Guo X, et al. Meta-analysis of genome-wide association studies in African Americans provides insights into the genetic architecture of type 2 diabetes. PLoS Genet 2014;10:e1004517. 25102180.

52. Saxena R, Saleheen D, Been LF, Garavito ML, Braun T, Bjonnes A, et al. Genome-wide association study identifies a novel locus contributing to type 2 diabetes susceptibility in Sikhs of Punjabi origin from India. Diabetes 2013;62:1746–1755. 23300278.

53. Cui B, Zhu X, Xu M, Guo T, Zhu D, Chen G, et al. A genome-wide association study confirms previously reported loci for type 2 diabetes in Han Chinese. PLoS One 2011;6:e22353. 21799836.

54. Wei C, Lu Q. Collapsing ROC approach for risk prediction research on both common and rare variants. BMC Proc 2011;5(Suppl 9):S42. 22373267.

55. Wu C, Walsh KM, Dewan AT, Hoh J, Wang Z. Disease risk prediction with rare and common variants. BMC Proc 2011;5(Suppl 9):S61. 22373337.

56. Eleftherohorinou H, Wright V, Hoggart C, Hartikainen AL, Jarvelin MR, Balding D, et al. Pathway analysis of GWAS provides new insights into genetic susceptibility to 3 inflammatory diseases. PLoS One 2009;4:e8068. 19956648.

57. Qian DC, Han Y, Byun J, Shin HR, Hung RJ, McLaughlin JR, et al. A novel pathway-based approach improves lung cancer risk prediction using germline genetic variations. Cancer Epidemiol Biomarkers Prev 2016;25:1208–1215. 27222311.

Supplementary materials

Supplementary data including two tables and one figure can be found with this article online http://www.genominfo.org/src/sm/gni-14-138-s001.pdf.

Supplementary Table 1

Genetic loci associated with T2D after adjusting for age, sex, area, and BMI (p < 5.00×10⁻⁰⁵)

gni-14-138-s001.pdf

Supplementary Table 2

List of SNPs reported by a GWAS catalog

gni-14-138-s002.pdf

Supplementary Fig. 1

Results of single-variant analysis for 344,893 SNPs in KARE cohort. (A) QQ plot of p-values derived from logistic regression with adjustments for Age, Sex, Area, and BMI. The shaded region represents the 95% confidence interval around the null hypothesis. (B) Manhattan plot of association p-values for T2D. The x-axis indicates the physical position of each genetic variant, and y-axis plots –log10(p-value). The genome-wide significance level is set to 1.45 × 10⁻⁰⁷ and is plotted as a red dotted line. SNP, single-nucleotide polymorphism; KARE, Korean Association Resource; QQ, quantile-quantile; BMI, body mass index; T2D, type 2 diabetes.

gni-14-138-s003.pdf

Article information Continued

(open-access, http://creativecommons.org/licenses/by-nc/4.0/) :

It is identical to the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/).

Group	Total individuals	T2D group	Normal group
KARE cohort
No. of subjects	8,842	1,042	2,943
Sex (male/female)	4,183/4,659	539/503	1,355/1,588
Age	52.2 ± 8.9	56.4 ± 8.6	51.1 ± 8.6
BMI	24.6 ± 3.1	25.5 ± 3.3	24.1 ± 2.9
Area (Anseong/Ansan)	4205/4,637	531/511	1,669/1,274
Health2 cohort
No. of subjects	1,816	794	770
Sex (male/female)	859/957	370/424	367/403
Age	60.7 ± 6.6	58.5 ± 7.2	63.6 ± 4.2
BMI	24.7 ± 3.3	25.3 ± 3.2	23.9 ± 3.2
HEXA cohort
No. of subjects	3,696	318	2,841
Sex (male/female)	1,647/2,049	203/115	1,120/1,721
Age	53.2 ± 8.3	58.6 ± 8.0	52.2 ± 8.1
BMI	24.0 ± 2.9	24.8 ± 2.9	23.7 ± 2.8

Variable	β	Region	Gene	Variable	β	Region	Gene
rs2236208	14.23	Intron	-	rs3773506	0.25	UTR-3	PLS1
rs2236207	−13.88	UTR-5	CSTF1	rs515071	−0.24	Intron	-
rs2700396	13.78	Intron	MYLK	rs10115450	−0.23	Intron	GRIN3A
rs13094803	−13.56	Intron	MYLK	rs2106294	−0.23	Intron	-
rs9939609	2.14	Intron	FTO	rs6813195	−0.21	down	-
rs9460546	2.10	Intron	CDKAL1	rs1525739	−0.21	Down	AGR3
rs8050136	−2.07	Intron	FTO	rs360481	−0.20	Intron	-
rs10946398	−2.02	Intron	CDKAL1	rs8181588	−0.20	intron	KCNQ1
rs11065756	−1.16	Intron	CCDC63	rs623323	0.20	down	NXN
rs10849915	0.88	Intron	CCDC63	rs5015480	0.19	Down	-
rs2074356	−0.75	Intron	C12orf51	rs10906115	−0.19	Up	CAMK1D
rs11066280	0.58	Down	RPL6	rs3132524	−0.19	Intron	POU5F1
rs6439472	0.43	Up	-	rs5215	0.18	Missense	KCNJ11
rs11086668	0.37	Intron	ZNF831	rs1048886	0.17	Missense	C6orf57
rs6665139	−0.34	Down	-	rs679992	−0.17	Intron	RGS7
rs10258075	0.34	Intron	INSIG1	rs17797882	−0.16	Down	MAF
rs3796439	−0.33	Intron	BMPR1B	rs6930576	0.16	Intron	SASH1
rs2444728	0.32	Down	-	rs7403531	0.15	Intron	RASGRP1
rs16841450	0.31	Intron	GALNT5	rs1436955	−0.14	Down	C2CD4B
rs6128654	0.31	Intron	PHACTR3	rs1495377	0.12	Intron	TSPAN8
rs9465871	−0.30	Intron	CDKAL1	rs1861612	0.11	Intron	DNER
rs1801282	−0.30	Intron	-	rs831571	−0.11	Up	-
rs2383208	−0.28	Down	-	rs17045328	0.11	Intron	CR2
rs773506	−0.26	Down	AUH	SEX	0.42	-	-
rs6882351	−0.26	Up	-	AREA	−1.05	-	-
rs470089	0.25	Intron	SULT4A1	AGE	0.11	-	-
rs7163430	−0.25	Up	SPRED1	BMI	0.20	-	-
rs4402960	0.25	Intron	IGF2BP2

SNP set	Description	GWAS catalog		KARE	No. of total variants
SNP set	Description	Population	p₁	p₂	p
ALL	Only reported SNPs in GWAS catalog	All populations	65	-	65
ASIAN	Only reported SNPs in GWAS catalog	Asian population	25	-	25
KARE	Only top SNPs in KARE cohort	-	-	100	100
ALL ＋ KARE	GWAS catalog ＋ KARE	All populations	65	35	100
ASIAN ＋ KARE	GWAS catalog ＋ KARE	Asian population	25	75	100

SNP set	Variable selection method	One set	Two set	Three set	Four set	Five set
ALL	SLR	3	3	1	-	-
	LASSO	6	4	3	2	1
	EN	6	6	5	3	2
ASIAN	SLR	3	3	1	-	-
	LASSO	6	4	3	2	1
	EN	6	6	6	2	1
KARE	SLR	80	59	55	47	37
	LASSO	82	75	63	56	48
	EN	100	100	77	68	54
ALL ＋ KARE	SLR	72	55	44	39	29
	LASSO	84	74	61	52	37
	EN	100	85	73	59	44
ASIAN ＋ KARE	SLR	78	59	50	42	31
	LASSO	83	76	70	62	50
	EN	83	76	70	62	50

SNP set	Variable selection method	Set (No. of SNPs)	Prediction method	No. of SNPs	AUC
SNP set	Variable selection method	Set (No. of SNPs)	Prediction method	No. of SNPs	KARE testing dataset	External replication dataset
Only demographic variables	-	-	-	-	0.715	0.561
ALL	EN	Two set (6)	EN	6	0.724	0.604
ASIAN	SLR	Two set (3)	LASSO	3	0.722	0.601
KARE	SLR	Three set (55)	LASSO	53	0.816	0.590
KARE	SLR	Three set (55)	EN	53	0.816	0.590
KARE	SLR	Five set (37)	LASSO	37	0.801	0.620
KARE	SLR	Five set (37)	EN	37	0.801	0.620
ALL ＋ KARE	EN	One set (100)	SLR	51	0.774	0.726
ALL ＋ KARE	SLR	One set (72)	SLR	51	0.772	0.726
ASIA ＋ KARE	EN	One set (83)	LASSO	71	0.809	0.599
ASIA ＋ KARE	EN	One set (83)	EN	71	0.809	0.599
ASIA ＋ KARE	SLR	Three set (50)	SLR	49	0.800	0.694