A semi-automatic cell type annotation method for single-cell RNA sequencing dataset

Article information

Genomics Inform. 2020;18.e26

Publication date (electronic) : 2020 September 8

doi : https://doi.org/10.5808/GI.2020.18.3.e26

Wan Kim, Sung Min Yoon, Sangsoo Kim

Department of Bioinformatics and Life Science, Soongsil University, Seoul 06978, Korea

^*Corresponding author: sskimb@ssu.ac.kr

Received 2020 March 11; Revised 2020 March 26; Accepted 2020 March 27.

Abstract

Introduction

Next-generation sequencing technology has transformed transcriptomics by allowing simultaneous identification and quantification of the expressed RNA molecules. However, this RNA-sequencing applied to bulk samples provides averaged expression profiles, not single-cell level variations. On the other hand, single-cell RNA-seq (scRNA-seq) isolates single cells from a given bulk sample, and measures the expression profile of a number of RNA species from each cell, offering the potential of cell-type characteristics as well as cell-type profiles of the bulk sample [1-3]. scRNA-seq has been applied to various fields such as neurobiology and cancer biology [1]. For example, immunotherapy has been developed as an effective cancer therapy, and thus underpinning of cancer immunology is crucial in the development of immunotherapy; scRNA-seq is a useful tool in this area [4-6].

scRNA-seq involves simultaneous analyses of many cell and genes, efficiency is crucial. One of the time-consuming steps is cell type annotation. The conventional method is laborious and subjective. To address this problem, some annotation methods have been developed by using additional transcriptomic data as reference coupled with machine-learning technique [7,8]. For instance, SingleR, a cell type annotation tool for scRNA-seq, leverages reference transcriptomic datasets of pure cell types to infer the cell of origin of each of the single cells independently [7]. But these methods require additional data and consume much computing power needed to perform machine-learning. Here we propose a semi-automatic method that calculates a normalized score for each cell type based on user-supplied cell type–specific marker gene list. The user can easily decide a cut-off score for each cell type based on the plots of score distributions.

Methods

Overall analysis workflow

Our scRNA-seq analysis pipeline is based on a well-established practice of processing 10× Genomics data. The sequencing data were processed with Cellranger to obtain an expression matrix of RNAs for each cell. Subsequent processing was performed with Seurat for various quality control steps involving cell filtering, normalization, and removal of technical variation, followed by preliminary analyses such as dimension reduction, clustering, cell type annotation, and differential expression analysis [11]. Our Cell Type Activity (CTA) annotation method is an alternative to the cell type annotation step in Seurat. For each cell type, the expression matrix of gene-by-cell was used in co-expression network analysis using WGCNA [12]. The modules in the network were analyzed for the enrichment of Gene Ontology terms and identification of upstream transcription factors (TFs) using iRegulon (Fig. 1) [13].

Fig. 1.

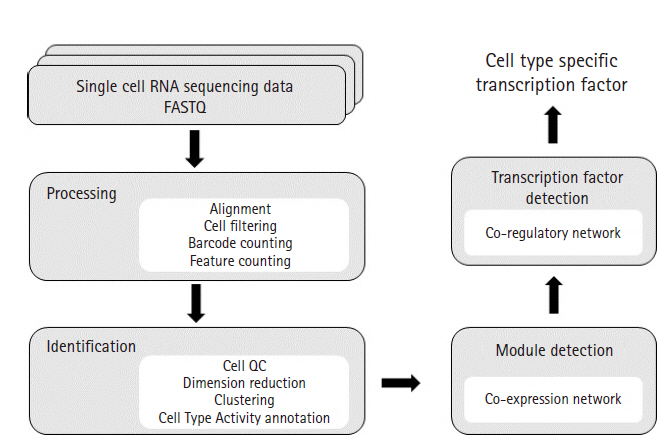
Analysis workflow diagram. This diagram illustrates overall workflow used in our study. FASTQ files were processed for alignment, cell filtering, UMI count and feature (genes) count by using CellRanger. CellRanger is a popular pipeline that processes Chromium single-cell 3′ RNA-sequencing data. Next, Seurat was used to generate clusters of cells. Seurat is an R package offering functions for secondary analysis such as cell QC, dimension reduction, clustering and differential expressed gene analysis. After clustering, we used our Cell Type Activity estimation technique for cell type annotation. To identify modules from each cell type, WGCNA was used. WGCNA is an R package that calculates correlation weighted network by using gene expression data and creates clusters of genes. Enrichment analysis study was conducted on each modules and iRegulon was used to identify potential transcription factors co-regulating the gene sets.

Results

The FASTQ files of mouse cardiac cell pools (ArrayExpress E-MTAB-6173) were processed with Cellranger, resulting in the feature-barcode matrix of 11,701 cells. Seurat was used to analyze the single-cell level heterogeneity. The cells having mitochondrial RNAs more than 25% of the total expressed RNAs were removed. In order to remove cells having unrealistic RNA varieties, only the cells with unique feature counts within the range between 200 and 5,000 were kept, resulting in a total of 11,587 cells and 17,432 genes. For the t-SNE clustering, 24 dimensional components as inferred from the principal component analysis and the resolution value of 2.0 were used, resulting in a total of 35 clusters. In order to annotate an appropriate cell type to each cluster we employed the CTA method (see Methods) using 12 cell types having 10 unique marker genes per cell type (Supplementary Table 1) [9]. The CTA score distribution for each cell type was manually examined to adjust the cut-off (see Supplementary Fig. 1A–F for exemplary plots). The t-SNE clustering with the cell type annotation is shown in Fig. 2, while the number of cells and genes identified for each cell type are listed in Table 1. The CTA matrix (12 rows by 35 columns) is given in Supplementary Table 2.

Fig. 2.

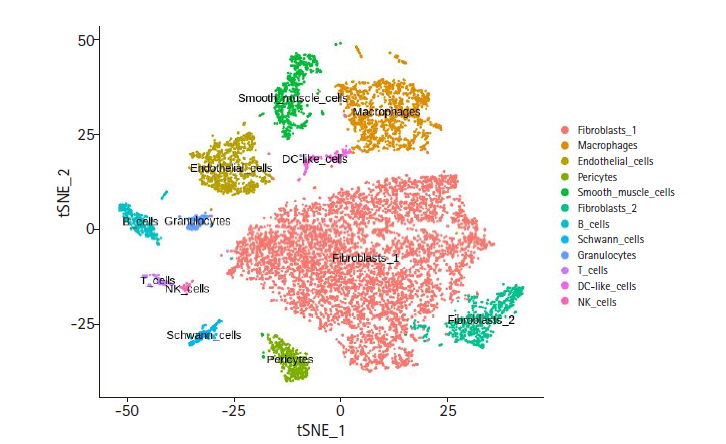
t-distributed stochastic neighbor embedding (t-SNE) result of cardiac non-myocytes. This plot displays final cell type annotation based on Cell Type Activity (CTA) scores. Feature-barcode matrix from single-cell RNA sequencing data was used for dimension reduction by using principal component analysis. After dimension reduction, t-SNE was used to visualize the clusters. The cell type for each cluster was inferred from the CTA score.

Table 1.

Annotation summary table

The performance of our CTA annotation method was evaluated with the other scRNA-seq dataset of mouse small intestinal epithelium [10]. The same workflow was applied for cell QC, resulting in a total of 5,188 cells and 14,259 genes. For clustering and visualization, 12 principal components and the resolution value of 0.8 were used, resulting in a total of 15 clusters. We performed the CTA method by using the 11 cell-type lists (Supplementary Table 3). Cumulative distribution of the CTA score was visualized for decision of the cut-off (Supplementary Fig. 2A–K). The final annotation graph visualized by t-SNE is shown in Supplementary Fig. 3, and the CTA matrix is given in Supplementary Table 4. The annotation results for the major clusters were qualitatively congruent with the original work [10].

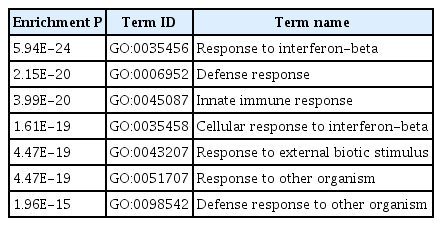
In order to assess the quality of our CTA annotation method, we performed co-expression and co-regulatory network analyses with the clustering and annotation results of the mouse cardiac cell pools [9]. While the member cells in each cell-type cluster display a similar expression profile as they are clustered together, their expression profiles are not identical to one another, and in fact they show some discrepancy as shown by the volume encompassed by each cluster (Fig. 2). This variation within a cell-type cluster may be an ideal resource for inferring co-regulatory networks. If our CTA method performed well, the resulting network should have reasonable literature evidence congruent with the annotated cell type. For each of the 12 cell-type clusters, co-expression network was constructed with WGCNA. The network was modularized using the soft threshold value (Supplementary Table 5) that produced a scale-free network for each cell-type cluster. Each co-expression module was further analyzed for the enrichment of Gene Ontology terms (Table 2).

Table 2.

Co-expression module summary table

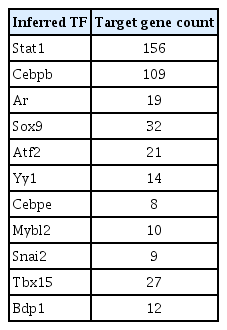
As shown in Table 3, an exemplary module from the dendritic cell (DC) cluster was significantly enriched with immune-related terms that are related to the features of dendritic cells such as immune cell activation, recognition of pathogen (the full listing in Supplementary Table 6). This module comprises of 242 genes and the iRegulon motif analysis of their 20 kb upstream of transcription start site inferred 11 potential TFs (Table 4). Among the inferred TFs, STAT1 and CEBPB have more than 100 target genes each. Their regulatory relationship is depicted in Fig. 3, showing that CEBPB regulates STAT1, which is also self-regulated. Having established this, their roles in DC biology was surveyed from the literature. It is known that up-regulation of STAT6 pathway plays an important role in the differentiation of immature DCs, and its down-regulation is related to the maturation of DCs. It is reported that STAT1 pathway works opposite to STAT6 pathway, maturating mDCs [16]. IRF8, an epigenetic and fate-determining TF of plasmacytoid dendritic cell (pDC), modulates chromatin modification of thousands of pDC enhancers. CEBPB forms a negative feedback loop with IRF8, determining the epigenetic fate of monocyte-derived DCs [17].

Table 3.

Dendritic cell exemplary module GO term result

Table 4.

Dendritic cell inferred TF summary table

Fig. 3.

Dendritic cell exemplary module regulatory network. Co-expression network was conducted to find modules of dendritic cell. Gene list in the module that highly enriched immune functions was analyzed to identify co-regulating transcription factors. Network visualization illustrates interactions between transcription factors (TFs; green) and genes (pink) from the module. The analysis revealed that two TF (CEBPB and STAT1) are significantly related to the genes. There is also relationship between two TFs and self-regulatory loop for the downstream STAT1.

Discussion

Here we propose an efficient semi-automatic processing pipeline of scRNA-seq data, called CTA method. Its quality was assessed by constructing co-expression and co-regulatory networks using the cell type annotation results. Our results were qualitatively congruent with the literature information. In scRNA-seq, many really expressed RNA species are missed. If this drop-out event can be complemented by imputation, much richer information can be retrieved. However, the current implementation of the imputation such as BISCUIT is very slow and not attempted in this work [18].

The strategy demonstrated in this work may find useful applications in inferring regulators of various cell types. For example, for the cell types whose critical differentiation regulators are elusive, co-regulatory network construction of progenitor and differentiated cells may elucidate key modules for the differentiation.

Supplementary Materials

Article information Continued