Review of Biological Network Data and Its Applications
Article information
Abstract
Studying biological networks, such as protein-protein interactions, is key to understanding complex biological activities. Various types of large-scale biological datasets have been collected and analyzed with high-throughput technologies, including DNA microarray, next-generation sequencing, and the two-hybrid screening system, for this purpose. In this review, we focus on network-based approaches that help in understanding biological systems and identifying biological functions. Accordingly, this paper covers two major topics in network biology: reconstruction of gene regulatory networks and network-based applications, including protein function prediction, disease gene prioritization, and network-based genome-wide association study.
Introduction
Network representations have been used to describe interactions between entities of interest in various areas. In particular, network representations are useful to analyze and visualize complex biological activities. Global patterns in a large-scale complex system can be shown by representing the entities and their interactions with nodes and edges, respectively. For instance, Schwikowski et al. [1] created protein-protein interaction (PPI) networks to predict novel protein functions in yeast Saccharomyces cerevisiae. By using the network representations, it was found that 2,358 among 2,709 total interactions compose a single large network. Also, biological pathway databases, such as Kyoto Encyclopedia of Genes and Genomes (KEGG) [2] and Reactome [3], provide numerous pathways that are represented by networks with nodes of molecules and directed edges of their actions. In addition, various mathematical properties and models of a network have been developed in graph theory. Several reviews [4-6] have illustrated the mathematical properties and topological characteristics of a network with biological systems.
The advance of high-throughput technologies, including DNA microarray [7], next-generation sequencing [8], and the two-hybrid screening system [9], has led to the large-scale datasets in genomics and proteomics, which are referred to as 'omics' data. These omics data have been collected and organized to identify biological functions. This paper focuses on biological network analysis related to omics data, such as gene expression levels and PPIs. We first report several major public interaction databases for the omics data and then introduce two major topics in network biology: reconstruction of gene regulatory networks (GRNs) and network-based applications, including protein function prediction, disease gene prioritization, and network-based genome-wide association study.
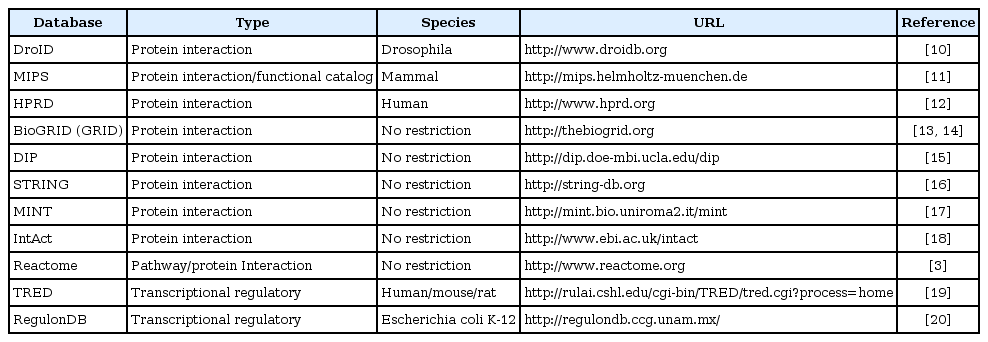
Network Resources
Experimental results from high-throughput technologies, such as the two-hybrid screening system for detecting interactions between biological molecules, have formed various types of network datasets that are released and updated in public databases on the web. These databases commonly enable web-based searches and provide raw datasets of pairs of molecules. In this review, we report 11 useful public databases for PPIs and transcriptional regulatory interactions (Table 1) [10-20]. For PPIs, BioGRID [13], MIPS [11], and STRING [16] are the most frequently used to predict protein functions for PPIs. BioGRID provides 496,761 non-redundant PPIs for various species, ranging from yeast S. cerevisiae to human. On the other hand, MIPS not only provides mammalian PPIs but also offers the functional catalogs that contain descriptions of protein functions. Unlike BioGRID and MIPS, STRING contains identified and predicted functional interactions of proteins with functional similarity scores (i.e., STRING offers weighted networks). For transcriptional regulatory interactions, transcriptional regulatory element database (TRED) [19] offers GRNs and transcriptional factors for three species; human, mouse, and rat. On the other hand, RegulonDB [20] contains both experimental datasets and computational prediction results of transcriptional regulatory interactions for the Escherichia coli K-12 organism.
Statistical Reconstruction of the Gene Regulatory Network from Gene Expression Data
Biological networks are generally constructed using known interactions identified from previous experiments. To integrate these separate pieces of information in the literature, text mining methods [21-24] have been proposed and used in the majority of public databases explained in the previous section. Although most biological networks are based on identified interactions under many different conditions and properties, GRNs can be constructed from gene expression datasets from a user's experimental datasets that implicitly contain gene regulation information in specific conditions (e.g., disease-specific, tissue-specific, or drug-specific GRNs). Most recently, the Encyclopedia of DNA Elements (ENCODE) project [25] produced numerous RNA-sequencing (RNA-seq) datasets that can provide gene expression levels and chromatin immunoprecipitation-sequencing (ChIP-seq) datasets that directly contain information about transcription factors (TFs). Integrative methods for reconstructing GRNs [26, 27] have been developed with the ENCODE [25] and modENCODE [28] project datasets. But, we focus on statistical approaches to reconstruct GRNs with gene expression datasets. Readers can refer to [26, 27] to read the details of reconstructing GRNs with ENCODE project datasets.
Many statistical approaches that infer networks from gene expression datasets have been developed. In this section, we briefly introduce four approaches to reconstruct GRNs: Gaussian graphical model, Bayesian network, correlation network, and information theory. Table 2 summarizes the methods described in this section with implementation languages and available URLs. A comparison study of several methods in these approaches has been published [29]. We remark that this review covers recent methods of the Gaussian graphical model and information theory approaches.
Gaussian graphical model
To cover the basic principle behind the Gaussian graphic model, let G = (V, E) be an undirected graph with a set V of nodes and a set E of edges and X = (X1, X2, … , Xp) = (X1, X2, …, Xn)T be an n × p dimensional design matrix, where Xj denotes a j-th variable and Xi denotes an i-th sample. In the Gaussian graphical model, it is assumed that an observation is from a p-dimensional multivariate normal distribution with mean zero and covariance matrix Σ (i.e., Xi~N(0, Σ) for i=1, 2,…, n). From this normality assumption, Xi and Xj are conditionally independent if (Σ-1)ij = 0 [30]. With this property, the Gaussian graphical model represents a conditional dependency between two variables into an edge (i.e., (i, j) ∈ E if (Σ-1)ij ≠ 0). Thus, we can obtain a network structure by estimating the inverse of covariance matrix (Σ-1), which is called a precision matrix. It is known that the maximum likelihood estimator (MLE) of the precision matrix is an inverse matrix of the sample covariance matrix. However, for high-dimensional data (p > n), the MLE of the precision matrix can not be obtained from the sample covariance matrix, since the sample covariance matrix is singular.
To resolve this problem and obtain the sparse solution, l1-regularized methods have been developed. These methods can be categorized into four types: regression-based [31, 32], penalized likelihood [33-38], empirical Bayes [39], and constrained l1 minimization [40]. We briefly introduce a recently developed example for each type of method. First, the sparse partial correlation estimation (SPACE) method [32] jointly solves p regression problems with l1 norm penalty on partial correlations. SPACE performs well in the detection of hub nodes that have many connections with other nodes. Unlike regression based-methods, the penalized likelihood-based methods directly maximize a likelihood function with positive definite constraints and l1 norm penalty on elements of the precision matrix. This maximization problem, proposed by [33], is more difficult to solve than the regression problem. To efficiently solve this problem, Friedman et al. [38] developed the graphical lasso algorithm that is motivated from [34, 35] and faster than other existing methods. In the empirical Bayes-based methods, Schafer and Strimmer [39] proposed the GeneNet method, based on multiple testing procedure on the partial correlations estimated by the Moore-Penrose pseudo inverse and the bootstrap method. Finally, Cai et al. [40] recently proposed constrained l1-minimization for inverse matrix estimation (CLIME), which directly minimizes the l1-norm of the precision matrix with a constraint for relaxation of the precision matrix condition.
Bayesian network
A Bayesian network is a probabilistic framework for representing a directed acyclic graph (DAG) structure, while Gaussian graphical models consider undirected graph structures. With the structure of DAG, the joint probabilities can be explicitly calculated from a simple conditional distribution. To obtain the network structure, Bayesian network methods generally select the graph structure by following three steps. Step 1-a candidate DAG structure is chosen among all possible DAG structures. Step 2-the posterior probability of the candidate DAG structure, given the gene expression data, is calculated. Step 3-repeat steps 1 and 2 until the highest posterior probability is obtained. Thus, searching candidate DAG structures becomes a critical part of the Bayesian network methods when the number of nodes increases. To avoid this problem, many heuristics are applied to improve efficiency [41-43]. For instance, B-Course [41], which is a web-based application, uses a combination of stochastic and greedy search, and BNT [42] and Werhli's Bayesian network [43] adopt Markov Chain Monte Carlo (MCMC) methods to find the best network structure for given gene expression data.
Correlation network
Correlation networks represent pairwise correlations between two nodes into edges. Although the construction of correlation networks can be straightforward to obtain from Pearson's correlations, it leads to a problem-that all the edges in the network are connected, since these correlations are generally non-zero. Thus, it is required that meaningless relationships in the correlation network be removed to focus on important edges that highly correlate nodes. To remedy this problem, hard thresholds [44] or soft thresholds [45] are applied to Pearson's correlations. By using threshold cutoffs, correlation network methods can capture biologically meaningful relationships. Moreover, this representation, based on correlations, is useful not only to identify modules of genes but also to interpret regulation interactions. "WGCNA" [46], an R implemented package, is an example that makes use of correlation networks. WGCNA provides the construction of unweighted (or weighted) networks with hard and soft threshold schemes [44, 45]. In addition, WGCNA offers various functions to analyze the network, including module detection, calculation of topological properties, and visualization.
Information theory
Information theory-based methods construct the GRN, based on information theoretic scores, such as the mutual information (MI), to measure dependencies between variables [47-50]. Unlike correlations, the MI does not assume the linearity and the continuity of variables. Thus, information theory-based methods generally outperform other methods that are based on correlation coefficients when the true network structure contains non-linearity dependencies. We first review two popular methods that reconstruct GRNs based on MI values and then introduce recently developed methods.
The relevance network method [47] uses the MI values to determine the edges in the GRN. To select significant edges, the relevance network proposes a threshold rule based on the distribution of the permuted MI values. The maximum value of the average of the permuted MI values is considered the threshold value. On the other hand, ARACNE [48, 49] additionally takes into account data processing inequality (DPI), in which the MI value of an indirect interaction is less than or equal to each MI value of the direct interactions for all triplets of nodes that only have two direct interactions. This DPI enforces that ARACNE [48, 49] discards indirect interactions and some direct interactions with small MI values.
To improve the accuracy of the information theory-based methods, the context likelihood of relatedness (CLR) algorithm [50] and the gene expression and transcription factor activity-based relevance network (GTRNetwork) algorithm [51] have been developed. These methods focus on the transcriptional regulatory interactions between known TFs and their target genes. Instead of using the MI values directly, the CLR algorithm proposes a likelihood value based on z-scores derived from the empirical distribution of the MI values in order to adjust random noises in the MI values. In addition to the CLR algorithm, the GTRNetwork algorithm additionally considers transcription factor activities (TFAs) between TFs and target genes as a hidden layer. The GTRNetwork algorithm first estimates changes of TFAs with known TF-gene networks and then identifies transcriptional regulatory interactions between the estimated TFAs and genes with the CLR algorithm. More recently, Zhang et al. [52] described the transcription procedure with TFAs by using the ordinary differential equation. Unlike the GTRNetwork algorithm, the NARROMI algorithm considers the gene expression data for candidate TFs as the TFAs and solves the minimization of the absolute errors between inferred and observed expressions with l1-norm penalty on the strength coefficients, which is referred to as recursive optimization in [52]. The NARROMI algorithm proposes the linear combination of the MI values and the absolute values of estimated strength coefficients as the final scores to construct the GRN.
Network-Based Applications
From the advances of high-throughput technologies, large-scale networks have been identified and are available from various public databases, as summarized in Table 1. In this section, we focus on network-based applications, especially how to use previously identified network resources in order to obtain meaningful biological interpretations. We first introduce three basic concepts in graph theory [53] to give an overview of the basic concepts of the network-based methods. First, a neighborhood of a node is a set of nodes connected to the node. Second, the distance between two nodes is defined as a length of the shortest path between them if the path exists; otherwise, it is set to infinity. Finally, an adjacency matrix is a binary and symmetric matrix such that its ij-th element is equal to 1 if there is an edge from a node i to a node j; otherwise, it is 0. In some cases, a weighted adjacency matrix can be used to represent the strengths of edges that usually fall between 0 and 1. With these basic concepts, we introduce three network-based applications: protein function prediction, disease gene prioritization, and genome-wide association study.
Protein function prediction
With the results of sequencing genomes, the efforts to predict protein functions have been focused on the functionalities of genomic annotations. In the initial stage, the prediction of protein function begins with the sequence homologies to annotated proteins [54-57]. These methods have been successful, but 70% of proteins still remain unannotated [58]. Accordingly, various types of methods have been developed to characterize unannotated proteins. In this review, we introduce four approaches in protein function prediction, based on direct interactions in the network: neighborhood-based, graph-based, Bayesian, and Kernel-based approaches. The methods are summarized in Table 3 [10, 11, 13-16, 59-83].
In neighborhood-based approach, the proposed methods [1, 62, 63, 65] commonly consider the number of edges connected to annotated proteins in a neighborhood. The neighborhood counting method [1] only takes into account the frequencies of annotated proteins in the neighborhood and chooses the top three functions, with the calculated frequencies ranked in descending order for each protein. Other methods also have derived their own scores, such as χ2 statistics [62] and functional similarities [63, 65], based on the annotated protein information in the neighborhood. These methods choose a function with the highest score as a predicted function for each protein.
The graph-based approach is similar to the neighborhood-based approach, but the graph-based approach focuses more on how to label the unannotated proteins with graph theoretical properties, such as the distance and the adjacency matrix. The label assignment models have been proposed with the adjacency matrix [66] and the weighted adjacency matrix [67], respectively. Since these assignment problems are computationally intractable, the heuristic methods, such as the simple threshold rule or simulated annealing [84], have been applied. To avoid these computational problems, several propagation-flavored methods have been developed. First, the label propagation methods [69, 70] obtain the optimal assignments and the optimal combination of the weight matrices that reflects different types of networks. Second, the functional flow method [68] iteratively spreads the flow from the annotated protein to the unannotated proteins by connected edges. The functional flow score, defined as an amount of the flow, is the criterion of the prediction. Third, the sequential linear neighborhood propagation method [71] sequentially updates unlabeled proteins according to their shortest path distance to the set of labeled proteins. Finally, the neighbor relativity coefficient (NRC) method [72] derives the NRC score by integrating various graph topological properties, such as the shortest path distance, path connectivity, and common neighbors.
The Bayesian approach takes into account the posterior probabilities of binary label random variables to obtain the prediction from the observed network and annotated proteins. Markov random field (MRF)-based [85] methods [74, 75] have been proposed and modified to Bayesian MRF [77] recently. To predict protein functions, these methods commonly derive the marginal posterior probability of the binary label variable given other variables and then estimate the posterior probability by Gibbs sampling. In addition to MRF-based models, other probabilistic models [78-80] have been developed under hierarchical structures from gene ontology [64]-which provides gene product annotation data that are characterized into three categories: biological processes, cellular components, and molecular functions-with some models, such as the hierarchical binomial neighborhood model [79]. In particular, Jiang et al. [80] considered the auto-probit model with a weighted network information from STRING [16], and their auto-probit model also reflects the uncertainty of the annotation [64].
The Kernel-based approach considers the protein function prediction problem as a classification problem. To reflect network information into the classification state, the network information is converted into a kernel matrix. Lanckriet et al. [81] proposed the kernel-based support vector machine (SVM) method, which incorporates heterogeneous types of data, such as amino acid sequence, gene expression data, and PPI network data, by converting these data into kernel matrices. The SVM method can be reformulated as semi-definite programming (SDP) [86] with kernels. Although the SVM method performs well, this method becomes slow when the dimension increases, caused by the computational complexity of the SDP. To remedy this problem, Lee et al. [82] proposed the kernel-based logistic regression (KLR) method by combing MRF-based methods [74, 75] with the diffusion kernel [87]. The KLR can contain multiple functions and various types of datasets at once. It has been shown that the KLR method is faster than the SVM and is comparable to the SVM in prediction accuracy [82]. Recently, Wang et al. [83] proposed the function-function correlated multi-label method, which treats all function categories in the prediction at once, while other methods only consider one function at a time, except for KLR.
Disease gene prioritization
Disease-gene association studies have focused on identifying relationships between disease phenotypes and genes to reveal and understand human disease mechanisms. Although traditional approaches, including linkage analysis and association studies, have been successful, the specified genomic intervals often contain tens or even hundreds of genes. It may not be possible by experiments to identify the correct causative genes of all the genes that lie on the specified intervals. To reduce experimental costs and efforts, the prioritization of candidate genes becomes one of the major tasks in disease-gene association studies.
Taking into consideration that genes corresponding to similar disease phenotypes tend to be neighbors in either a PPI network [88, 89] or a pathway [90], several network-based disease gene prioritization methods have been proposed recently. The network-based disease gene prioritization methods [91-94] define different similarity scores between the disease and genes, based on either functional annotations or PPI networks, to rank candidate genes. The random walk method [91] considers the random walk on graphs and uses a diffusion kernel matrix [87] derived from a PPI network as the steady-state transition probability matrix. The random walk method then defines the similarity score as the sum of elements of the diffusion kernel corresponding to known disease genes for each candidate gene. CIPHER [92] adopts a regression model for similarities between phenotypes and considers the Gaussian kernel for closeness between genes. The Pearson correlation coefficient between the similarity of phenotypes and the closeness between genes is used as a similarity score. On the other hand, PRINCE [93] and MINProp [94] are based on the iterative label propagation algorithm [95]. PRINCE defines the prioritization function, which combines functional similarities from the network information with prior information for disease phenotypes as the similarity score. The prioritization function is obtained by iteratively applying a label propagation algorithm. MINProp first defines two heterogeneous networks, such as a gene network and a disease network, and then additionally defines bipartite networks between two heterogeneous networks from known disease-gene associations. After initializing the labels of the disease genes, MINProp iteratively propagates label information through three networks until convergence occurs. Finally, the converged label scores are used as the similarity scores. From the comparison study in [93, 94], PRINCE and MINProp outperform the random walk and CIPHER methods, respectively. There is no comparison study between PRINCE and MINProp, but MINProp is more general than PRINCE, since MINProp can be applied to three or more heterogeneous networks. We report these disease gene prioritization methods with their data resources in Table 4 [12, 13, 15-18, 91-94, 96-99].
Genome-wide association study (GWAS)
The GWAS measures DNA sequence variations in the human genome to identify associations between genetic variants and diseases (or phenotypes). To measure genetic variations, the single- nucleotide polymorphism (SNP), which represents a single base-pair change in the DNA sequence, is generally used as a marker of a genomic region in the GWAS. Generally, the GWAS conducts a comparison of the SNPs between case and control groups (i.e., disease and non-disease groups) by statistical methods, such as ANOVA and logistic regression, to identify significant SNPs related to the disease. Genetic risk factors revealed by a GWAS can be used as preventive markers or for therapeutic targets in curing the disease. There have been more than 11,000 SNPs discovered as candidate bio-markers in common diseases [100]. The large number of SNPs detectable in the human genome can, however, lead to multiple testing problems. To control the false positive errors (i.e., type I errors in the context of statistical testing procedures), the Bonferroni correction and false discovery rate [101] methods are commonly adopted. Although these multiple testing rules have been successful in the identification of significant single SNPs, these test procedures often fail to detect genomic regions that are weakly associated with the disease and still ignore the combined effects caused by the interactions between genes.
The network-based GWAS methods [102-104], summarized in Table 5 [12, 13, 17, 102-114], take into account both interactions between genes or proteins with association information available from a GWAS. The HumanNet method [115] combines functional gene networks derived from multiple network sources, such as the PPI network, and mRNA co-expression with the log odds ratio from GWAS data to prioritize disease genes. By combining functional gene networks and the information from GWAS data, HumanNet has higher power to detect disease-related genes. Unlike HumanNet, NIMMI [116] and dmGWAS [117] focus on identifying groups of genes associated with diseases, based on GWAS data and PPI network data. NIMMI constructs a PPI network with weights of genes by using a modified Google PageRank algorithm [118]. The weights of genes are then combined with the gene-based association p-values calculated from GWAS data. The subnetworks of genes are identified by the DAVID method [119, 120] with the network structure and weights of genes. On the other hand, dmGWAS only considers gene-based association p-values as the node weights and proposes a modified version of the dense module searching method [121] to prioritize candidate groups of genes.
Discussion
We have reviewed a number of methods related to two topics in network data analysis: network reconstruction and network-based application. Network reconstruction can be thought of as a reverse-engineering problem whose goal is to rebuild true structures or relationships from observations. In particular, we focused on statistical methods for building GRNs, including the Gaussian graphical model, correlation network, Bayesian network, and information theory-based methods. Most methods that we have reviewed consider the sparsity on the graph structure to select a small number of significant dependencies between nodes. This sparsity condition is adequate for the network in biological systems, since it reflects a scale-free feature, where several nodes have many edges but the majority of nodes only has three or four edges [5]. Although most methods in Gaussian graphical models are well studied in their theoretical properties, these methods have limitations when applied to biological data. Since these methods basically assume a Gaussian distribution, they are only applicable for continuous-type datasets, such as gene expression levels. To construct networks from other types of data, such as binary or counts, the Bayesian network and information theory-based methods are more attractive than correlation-based methods.
Second, we introduced various methods in three network-based applications. Most methods consider similarity measures between nodes and then use these measures to predict biological functions or prioritize candidate genes associated with diseases. As technologies in the experiments progress, the network-based methods can be improved and widely extended. For instance, even though the neighborhood counting method [1] in protein function prediction only considers the count of annotated functions in the neighborhood from a PPI network, the recently developed methods [72, 83] can contain not only neighborhood information but also functional similarities from multiple networks. In addition, module-assisted methods that focus on identifying a functional group of proteins are also available and well summarized in [122]. Furthermore, the network-based tumor stratification (NBS) method has been developed recently [123]. This NBS method combines mutation profiles from The Cancer Genome Atlas (TCGA) projects [116, 117, 124, 125] and network information to obtain informative strata (e.g., subtypes of cancer). Although these network-based methods have been improved, these methods still lack accuracy compared with other methods [115]. Since the high-throughput data may contain many false positives [126], the network-based methods are affected in their accuracy. Although their performance depends on the quality of data, their effects are expected to decrease in the future as improvements are made in measurement accuracy.