 |
 |
- Search
| Genomics Inform > Volume 17(4); 2019 > Article |
|
Abstract
Isolation-with-migration (IM) models have become popular for explaining population divergence in the presence of migrations. Bayesian methods are commonly used to estimate IM models, but they are limited to small data analysis or simple model inference. Recently three methods, IMa3, MIST, and AIM, resolved these limitations. Here, we describe the major problems addressed by these three software and compare differences among their inference methods, despite their use of the same standard likelihood function.
Divergence between populations and species has been a major interest in population genetics and evolution. Estimating divergence from genetic data is difficult because of conflicting evolutionary processes. Genetic drift elevates divergence between populations or between species, while gene flow can remove signals of divergence [1]. An isolation-with-migration (IM) model is a widely used demographic model describing the two conflicting signals. A typical 2-population IM model with six parameters (Fig. 1) depicts two populations (sizes ╬Ė1 and ╬Ė2, respectively) that arise from a single ancestral population (size ╬Ėa) at time TS in the past, while the two populations may exchange migrants at rates m1 and m2 ([1-3] for notations). Both population sizes and migration rates are assumed to be constant over time [4].
The challenges of inferring isolation models (with no migrations) and even phylogeny have been addressed by using a multispecies coalescent framework [5-11]. However, ignoring migrations can result in a biased estimation of splitting times of populations/species and may lead to a wrong phylogenetic tree estimation [12-16]. Efforts to distinguish between isolation and migration began about 20 years ago, and many methods have employed a Markov chain Monte Carlo (MCMC) simulation to infer an IM model [2-4,17-21]. However, most methods have a major roadblock of a long computational time of an MCMC simulation, which typically limits the amount of data that can be analyzed [1]. In addition, the joint estimation of both phylogeny and an IM model is known to be tremendously difficult [16].
Recently, three methods have been developed to address the scalability of the data and/or to jointly infer phylogeny in the presence of gene flow. IMa3 [16] is the most recent version of IM/IMa series software and infers the phylogeny and IM models. MIST [1] needs a known (or assumed) phylogeny but is able to analyze thousands of loci. AIM [14,22] is a package in the popular BEAST platform and also infers phylogeny in the presence of gene flow. Similar to other methods, these three methods implement the standard probabilistic framework and employ an MCMC simulation for inference.
The advent of many inference methods is not commensurate to our skills of analysis using those programs. In order to ensure the use of appropriate programs and to correctly interpret results, it is essential to understand the inference methods used and the results that the programs provide. IMa3, MIST, and AIM all use similar standard probabilistic models and apply Bayesian inference, but their inference strategies and the types of results may be different. Therefore, users must first understand the differences in their inference methods.
To elucidate the current state of the art in the analysis of IM models, in this review article, we compare the three methods and accompanying software, IMa3, MIST, and AIM (BEAST platform). In particular, the data type and the underlying model structures will be discussed, followed by a brief summary of an MCMC algorithm and mixing issue. Then, this review article will focus on comparison of the advanced methods: IMa3, MIST, and AIM. We do not intend to explain the basic concepts of standard probabilistic models and MCMC algorithms, but extensive reviews of them are available elsewhere [9,23-25].
One of the most common types of data used in the analysis of IM models and phylogeny is DNA sequence alignments. Most methods, including IMa3, MIST, and AIM, assume the alignments are correct, although they are estimated from models of insertions and deletions [26]. The relatedness of homologous DNA sequences is considered to the result from past branching processes, so the DNA sequence alignments must be orthologs [22]. Moreover, no selection but a neutral evolution is assumed to act on alignments. Since most methods typically assume that there is no recombination within a locus and free recombination between loci, alignments should not overlap or be closely located. Moreover, filtering using a four-gamete test [27] is essential to minimize potential recombination within a locus.
When inferring an IM model from genetic data, the parameters of interest are demographic parameters of the IM model, denoted as a vector Žł=(╬Ė1, ╬Ė2, ╬Ėa, m1, m2, TS). The ith locus Di out of L loci are the observations, and the genealogy Gi of Di is a latent variable that we cannot observe typically (Fig. 2). Fig. 2 depicts the structure of the standard models. The standard models address two levels of uncertainty: the distribution of DNA sequences given genealogy and that of genealogy given an IM model [11,12,25]. We typically assume that there is no recombination within a locus and free recombination between loci. In other words, the ith locus Di out of L loci has as its own genealogy Gi and loci are independent. Given genealogy, the genetic data and demography Žł=(╬Ė1, ╬Ė2, ╬Ėa, m1, m2, TS) are assumed to be conditionally independent. As the distribution of DNA sequences p D i G i p G i Žł
A feasible way to numerically evaluate the likelihood function (Eq. 1) is an MCMC simulation. Extensive reviews of fundamental concepts, diverse algorithms, and MCMC diagnosis are available elsewhere [23,25,36,37]. With a prior distribution on Žł, the posterior density of Žł given data is
The target density of an MCMC simulation is p Žł , G 1 , ŌĆ” , G L D ŌłØ p ╬© ŌłÅ i = 1 L p D i G i p G i Žł Žł 1 , ┬Ā G 1 1 , ŌĆ” , G L 1 , Žł 2 , ┬Ā G 1 2 , ŌĆ” , G L 2 , ŌĆ” , Žł n , ┬Ā G 1 n , ŌĆ” , G L n ~ P Žł , ┬Ā G 1 , ŌĆ” , G L D
One of the benefits of such a simulation is an easy approximation of the marginal posterior density (Eq. 2) by making use of simulated values for the parameter of interest. For example, Žł 1 , ŌĆ” Žł n Žł 1 , ┬Ā G 1 1 , ŌĆ” , G L 1 , Žł 2 , ┬Ā G 1 2 , ŌĆ” , G L 2 , ŌĆ” , Žł n , ┬Ā G 1 n , ŌĆ” , G L n p Žł D
A popular MCMC algorithm is a Metropolis-Hastings within Gibbs sampling algorithm (Fig. 3). Within each iteration, all demographic parameters and genealogies are sequentially simulated. For example, Fig. 4A shows the state of the (t-1)th iteration for the genealogy of one locus and all demographic parameters Žł including splitting time T S t - 1 T S * T S t = T S * ╬▒ = min { 1 , p ( G t Žł * ) q ( T S t - 1 T S * ) p ( G t Žł t - 1 ) q ( T S * T S t - 1 ) } T S t = T S t - 1 T S * T S t - 1
While samples via a traditional Monte Carlo method are independent, MCMC samplers generate autocorrelated draws because the current value is either a different value or the same as the previous. Strong autocorrelations slow down traversing the posterior space and take longer to produce independent-like samples Žłt, ŌĆ” Žłn ~ p ( Žł D ) p G t Žł * = 0
The software series of IM/IMa were developed to infer IM models (Table 1) [39,40]. The first software, called IM, analyzes either a single locus [4] or multiple loci [2], and implements MCMC approaches to infer six demographic parameters ╬© = ( ╬Ė 1 , ╬Ė 2 , ╬Ė a , m 1 , m 2 , T S ) Žł , G 1 , ŌĆ” , G L ~ P Žł , G 1 , ŌĆ” , G L D T S , G 1 , ŌĆ” , G L ~ p T S , G 1 , ŌĆ” , G L D ŌłØ ŌłÅ i = 1 L p ( D i G i ) p ( G 1 , ŌĆ” , G L T S ) p T S
This yields a better mixing than software IM by reducing the number of parameters to sample, but it does not resolve the fundamental barrier of the relation between genealogies and splitting time. As a result of an MCMC simulation, the sampled values approximate the marginal posterior of the splitting time: T S 1 , ŌĆ” , T S n ~ p T S D p ( T S D ) p ( ╬Ė i D ) p ( m i D ) p ( m i D )
The most recent version called IMa3 modified the MCMC procedure of IMa2 to infer an IM model parameters as well as phylogeny [16], while IMa2 requires the phylogeny of multiple populations to be known. It is very difficult to co-estimate the phylogeny and IM model parameters, because sampling phylogeny together with IM parameters and genealogies also yields poor mixing. For example, a newly proposed phylogeny may not be compatible with the current state of migrations and is therefore rejected. IMa3 introduces pseudo-migrations, called ŌĆ£hidden migrations,ŌĆØ that occurred earlier than the splitting time so that a newly proposed splitting time or phylogeny is not instantly rejected but evaluated with non-zero acceptance probability. For example, if a newly proposed splitting time is younger than existing migrations (Fig. 4B), the migration paths older than splitting time are considered hidden migration paths (MH) and the genealogy is the one without hidden migrations and compatible with the new splitting time. In other words, the current genealogy, given the new splitting time, is a so-called ŌĆ£hidden genealogyŌĆØ GH=(G, MH). Given phylogeny Žä and demographic parameters Žł, the distribution of the hidden genealogy is partitioned into those of hidden migrations and the genealogy without hidden migrations: p ( G H Žł , Žä ) = p ( G Žł , Žä ) p m H Žł , Žä Žä 1 , T S 1 , G H , 1 1 , ŌĆ” , G H , L 1 , Žä 2 , T S 2 , G H , 1 2 , ŌĆ” , G H , L 2 , ŌĆ” , Žä n , T S n , G H , 1 n , ŌĆ” , G H , L n ~ P Žä , T S , G H , 1 , ŌĆ” , G H , L D ŌłØ p Žä p Žł ŌłÅ i = 1 L p D i G i p G i Žł , Žä p m H , i Žł , Žä
Then Žä1, ... , Žän from the MCMC samples approximately follow the marginal posterior p ( Žä D )
Software MIST [1] implements a 2-step analysis. First, it simulates genealogies without migrations (so-called coalescent trees ╬╗_) via an MCMC simulation. Note that no information about a demographic model is necessary in the first step, which alleviates the mixing problem. Second, the joint posterior density p ( Žł D )
Although MIST does not sample migrations and the underlying demographic model in step 1, the same posterior density p ( Žł D )
where the ith genealogy Gi=(╬╗i, Mi)and Mi is the set of all migration information. This rewrites Eq. (2) as follows:
The exact computation of p ╬╗ i Žł p ╬╗ i Žł p ~ ( ╬╗ i Ōöé D i ) ŌłØ p ( D i Ōöé ╬╗ i ) p ~ ( ╬╗ i ) p ╬╗ i Žł p ~ ╬╗ p ~ ╬╗ i D i p ╬╗ i Žł
As a result, MIST provides the MAP of all demographic parameters that maximize the joint posterior Eq. (6).
MIST has several strengths statistically and computationally. First, the computational complexity linearly increases with the number of loci. Analyses of thousands of loci do not give rise to mixing problems. Second, similar to IMa series, the approximate p(ŽłŌöéD) in Eq. (6) can be used for LRTs for migration rates. While the IM/IMa series uses the marginal
densities, MIST provides the joint distribution of all demographic parameters (Table 2). Since the estimations of demographic parameters are correlated, LRTs based on joint distributions have false-positive rates close to the expected value (e.g., 5%), even when very high false-positive rate occurred by LRTs based on marginal distributions [1,41,42]. Third, the importance sampling method enhances the computational efficiency for model comparisons. When different demographic models are compared, the simulated values from an MCMC simulation in step 1 can be repeatedly employed to infer different demographic models in step 2.
AIM [14] implements a Bayesian inference of phylogeny and IM models in using the BEAST platform [15,43]. BEAST is a software platform for phylogenetic analyses, phylodynamics, and population genetics. starBEAST2 [44], an extended BEAST package, was added to estimate species trees in the absence of gene flow. AIM was recently added to estimate the posterior density p Žł D p Žä D p ╬╗ i Žł P t L 1 = l 1 , L 2 = l 2 ╬╗ , Žł Ōēł P t L 1 = l 1 ╬╗ , Žł P t L 2 = l 2 ╬╗ , Žł
where L1 and L2 are lineages of ╬╗ at time t. AIM implements this independence approximation rather than the exact density p ╬╗ i Žł
AIM reparamerized migration rates as follows: migration rate between populations A and B, m A , B = ╬▒ A , B m t o t ╬┤ A B
AIM performs tests for migration rates based on Bayes factors (BFs) [14], while IMa3 and MIST use LRTs (Table 2). A BF as the ratio of marginal likelihoods [37] is wildely used for model selection. Since AIM is a package in the BEAST platform, users can take advantage of other existing packages and MCMC diagnostic tools. However, most packages in BEAST were developed independently [15,45]. Therefore, the results provided by different packages are not connected, and users need to be aware of the different terminologies by each package [15].
IMa3, MIST, and AIM are advanced software that estimate demographic parameters of IM models. IMa3 and AIM sample population tree topologies and all or partial demographic parameters through an MCMC simulation. Therefore, their estimations are based on the marginal posterior distribution of parameters. MIST can estimate the joint posterior distribution of all parameters, thereby providing a joint estimation. IMa3 and AIM estimate population tree topology and migration rates, but their scalability to genomic data is limited or has not been yet examined. MIST scales well with genomic data and can be extended to infer population tree topologies. However, the software currently supports a joint estimation of demographic parameters of 2-population IM models.
While AIM uses BFs for migration rate test, IMa3 and MIST suggest LRTs. While IMa3 compares marginal posterior distributions, MIST provides joint posterior distributions for LRTs. When splitting times are recent, it is important to consider using joint distributions for LRTs in order to avoid a high false-positive [1,41,42].
Long-standing barriers to inferring IM models have been resolved by IMa3, MIST, and AIM. MIST can analyze genome-scale data without sever mixing problems in an MCMC simulation. IMa3 and AIM are able to estimate IM models and phylogeny in the presence of migrations. Nonetheless, there are still unresolved questions and no software implementing sophisticated models to answer the questions. One of the major interests for the future is to relax the strong assumption of constant migration rates and population sizes over time. Current methods that attempt to solve this problem are limited to small data or not capable of inferring IM models from real genetic data analysis [46,47].
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2018R1C1B5044541).
Fig.┬Ā2.
Standard model structure. Each locus has its own genealogy. Given genealogy, the genetic data and demography are assumed to be independent.
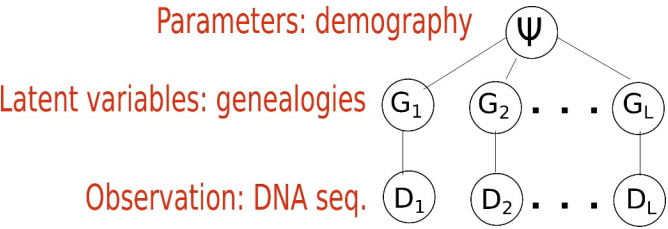
Fig.┬Ā4.
An example of an Markov chain Monte Carlo step to update the splitting time TS. (A) The current state of genealogy and all demographic parameters, including TS. (B) A newly proposed splitting new TS, which is not compatible with the state of genealogy.

Table┬Ā1.
Comparison of Bayesian software MIST, AIM, and IMa3 (IM/IMa series)
| Software | No. pop. to analyze | Inference method | Reference | |||
|---|---|---|---|---|---|---|
| ╬Ė's and mŌĆÖs | Ts | Ga | Žä | |||
| MIST | 2 | Density approx.b | Density approx.b | MCMC | No | [1] |
| AIM | 2 or more | MCMC | MCMC | MCMC | MCMC | [14,22] |
| IMa3 | 2 or more | Density approx.c | MCMC | MCMCd | MCMC | [16] |
| IM | 2 | MCMC | MCMC | MCMC | No | [2,4] |
| IMa | 2 | Density approx.c | MCMC | MCMC | No | [3] |
| IMa2e | 2 or more | Density approx.c | MCMC | MCMC | No | [3,17] |
MIST, AIM, and IMa3 are compared in terms of the number of populations to analyze and inference methods by indicating what Markov chain Monte Carlo (MCMC) samples and which parametersŌĆÖ posterior densities are approximated rather than sampled. A similar comparison is made with IM/IMa series.
Table┬Ā2.
Prior assumptions, migration rate tests and scalability of Bayesian software MIST, IMa3, and AIM
| MIST | IMa3 | AIM | ||
|---|---|---|---|---|
| Priors | ╬ĖŌĆÖs, | Uniform | Uniform | Log-normal [44] |
| mŌĆÖs | Uniform | Uniform | Exponetiala | |
| TS | Uniform | Uniform | Various [44] | |
| Žä | Uniform | Various [44] | ||
| Tests for | mŌĆÖs | LRTb | LRTc | Bayes factor |
| Scalabilityd | Loci | Many (Ōēż10K [1]) | Moderate (Ōēż200 [16]) | Moderate (Ōēż50 [14]) |
| Sequences | Few (Ōēż8 [1]) | Moderate (Ōēż40 [16]) | Moderate (Ōēż133 [22]) |
References
1. Chung Y, Hey J. Bayesian analysis of evolutionary divergence with genomic data under diverse demographic models. Mol Biol Evol 2017;34:1517ŌĆō1528.




2. Hey J, Nielsen R. Multilocus methods for estimating population sizes, migration rates and divergence time, with applications to the divergence of Drosophila pseudoobscura and D. persimilis. Genetics 2004;167:747ŌĆō760.



3. Hey J, Nielsen R. Integration within the Felsenstein equation for improved Markov chain Monte Carlo methods in population genetics. Proc Natl Acad Sci U S A 2007;104:2785ŌĆō2790.



4. Nielsen R, Wakeley J. Distinguishing migration from isolation: a Markov chain Monte Carlo approach. Genetics 2001;158:885ŌĆō896.




5. Drummond AJ, Suchard MA, Xie D, Rambaut A. Bayesian phylogenetics with BEAUti and the BEAST 1.7. Mol Biol Evol 2012;29:1969ŌĆō1973.




6. Kubatko LS, Carstens BC, Knowles LL. STEM: species tree estimation using maximum likelihood for gene trees under coalescence. Bioinformatics 2009;25:971ŌĆō973.



7. Liu L. BEST: Bayesian estimation of species trees under the coalescent model. Bioinformatics 2008;24:2542ŌĆō2543.



8. Liu L, Pearl DK. Species trees from gene trees: reconstructing Bayesian posterior distributions of a species phylogeny using estimated gene tree distributions. Syst Biol 2007;56:504ŌĆō514.



9. Liu L, Yu L, Kubatko L, Pearl DK, Edwards SV. Coalescent methods for estimating phylogenetic trees. Mol Phylogenet Evol 2009;53:320ŌĆō328.


10. Rannala B, Yang Z. Efficient Bayesian species tree inference under the multispecies coalescent. Syst Biol 2017;66:823ŌĆō842.



11. Degnan JH, Rosenberg NA. Gene tree discordance, phylogenetic inference and the multispecies coalescent. Trends Ecol Evol 2009;24:332ŌĆō340.


12. Chung Y, Ane C. Comparing two Bayesian methods for gene tree/species tree reconstruction: simulations with incomplete lineage sorting and horizontal gene transfer. Syst Biol 2011;60:261ŌĆō275.



13. Leache AD, Harris RB, Rannala B, Yang Z. The influence of gene flow on species tree estimation: a simulation study. Syst Biol 2014;63:17ŌĆō30.



14. M├╝ller NF, Ogilvie HA, Zhang C, Drummond A, Stadler T. Inference of species histories in the presence of gene flow. Cold Spring Harbor: bioRxiv, Cold Spring Harbor Laboratory, 2018. Accessed 2019 Aug 3. Available from: https://doi.org/10.1101/348391.

15. Bouckaert R, Vaughan TG, Barido-Sottani J, Duchene S, Fourment M, Gavryushkina A, et al. BEAST 2.5: an advanced software platform for Bayesian evolutionary analysis. PLoS Comput Biol 2019;15:e1006650.



16. Hey J, Chung Y, Sethuraman A, Lachance J, Tishkoff S, Sousa VC, et al. Phylogeny estimation by integration over isolation with migration models. Mol Biol Evol 2018;35:2805ŌĆō2818.




17. Hey J. Isolation with migration models for more than two populations. Mol Biol Evol 2010;27:905ŌĆō920.



18. Wakeley J, Hey J. Testing speciation models with DNA sequence data. In: Molecular Approaches to Ecology and Evolution (DeSalle R, Schierwater B, eds.). Basel: Birkh├żuser, 1998. pp. 157ŌĆō175.
19. Becquet C, Przeworski M. A new approach to estimate parameters of speciation models with application to apes. Genome Res 2007;17:1505ŌĆō1519.



20. Dalquen DA, Zhu T, Yang Z. Maximum likelihood implementation of an isolation-with-migration model for three species. Syst Biol 2017;66:379ŌĆō398.



21. Mailund T, Halager AE, Westergaard M, Dutheil JY, Munch K, Andersen LN, et al. A new isolation with migration model along complete genomes infers very different divergence processes among closely related great ape species. PLoS Genet 2012;8:e1003125.



22. M├╝ller NF, Rasmussen DA, Stadler T. The structured coalescent and its approximations. Mol Biol Evol 2017;34:2970ŌĆō2981.




23. Craiu RV, Rosenthal JS. Bayesian computation via Markov chain Monte Carlo. Annu Rev Stat Its Appl 2014;1:179ŌĆō201.

24. Sousa V, Hey J. Understanding the origin of species with genome-scale data: modelling gene flow. Nat Rev Genet 2013;14:404ŌĆō414.




25. Nascimento FF, Reis MD, Yang Z. A biologist's guide to Bayesian phylogenetic analysis. Nat Ecol Evol 2017;1:1446ŌĆō1454.




26. Chatzou M, Magis C, Chang JM, Kemena C, Bussotti G, Erb I, et al. Multiple sequence alignment modeling: methods and applications. Brief Bioinform 2016;17:1009ŌĆō1023.



27. Hudson RR, Kaplan NL. Statistical properties of the number of recombination events in the history of a sample of DNA sequences. Genetics 1985;111:147ŌĆō64.




28. Kimura M. The number of heterozygous nucleotide sites maintained in a finite population due to steady flux of mutations. Genetics 1969;61:893ŌĆō903.




29. Jukes TH, Cantor CR. Evolution of protein molecules. In: Mammalian Protein Metabolism (Munro HN, ed.). New York: Academic Press, 1969. pp. 21ŌĆō132.
30. Hasegawa M, Kishino H, Yano T. Dating of the human-ape splitting by a molecular clock of mitochondrial DNA. J Mol Evol 1985;22:160ŌĆō174.



31. Tavare S. Some probabilistic and statistical problems in the analysis of DNA sequences. Am Math Soc Lect Math Life Sci 1986;17:57ŌĆō86.
33. Hudson RR. Properties of a neutral allele model with intragenic recombination. Theor Popul Biol 1983;23:183ŌĆō201.


34. Hudson RR. Testing the constant-rate neutral allele model with protein sequence data. Evolution 1983;37:203ŌĆō217.


35. Felsenstein J. Phylogenies from molecular sequences: inference and reliability. Annu Rev Genet 1988;22:521ŌĆō565.


36. Yang Z. Molecular Evolution: A Statistical Approach. Oxford: Oxford University Press, 2014.
38. Robert CP, Casella G. Monte Carlo Statistical Methods. New York: Springer, 2004.
39. Sethuraman A, Hey J. IMa2p: parallel MCMC and inference of ancient demography under the Isolation with migration (IM) model. Mol Ecol Resour 2016;16:206ŌĆō215.


40. Knoblauch J, Sethuraman A, Hey J. IMGui-A Desktop GUI application for isolation with migration analyses. Mol Biol Evol 2017;34:500ŌĆō504.


41. Cruickshank TE, Hahn MW. Reanalysis suggests that genomic islands of speciation are due to reduced diversity, not reduced gene flow. Mol Ecol 2014;23:3133ŌĆō3157.


42. Hey J, Chung Y, Sethuraman A. On the occurrence of false positives in tests of migration under an isolation-with-migration model. Mol Ecol 2015;24:5078ŌĆō5083.



43. Bouckaert R, Heled J, Kuhnert D, Vaughan T, Wu CH, Xie D, et al. BEAST 2: a software platform for Bayesian evolutionary analysis. PLoS Comput Biol 2014;10:e1003537.



44. Ogilvie HA, Bouckaert RR, Drummond AJ. StarBEAST2 brings faster species tree inference and accurate estimates of substitution rates. Mol Biol Evol 2017;34:2101ŌĆō2114.




45. Barido-Sottani J, Boskova V, Plessis LD, Kuhnert D, Magnus C, Mitov V, et al. Taming the BEAST-A community teaching material resource for BEAST 2. Syst Biol 2018;67:170ŌĆō174.



- TOOLS
-
METRICS

-
- 3 Crossref
- 0 Scopus
- 5,727 View
- 131 Download
- Related articles in GNI









