Identifying Copy Number Variants under Selection in Geographically Structured Populations Based on F-statistics
Article information
Abstract
Large-scale copy number variants (CNVs) in the human provide the raw material for delineating population differences, as natural selection may have affected at least some of the CNVs thus far discovered. Although the examination of relatively large numbers of specific ethnic groups has recently started in regard to inter-ethnic group differences in CNVs, identifying and understanding particular instances of natural selection have not been performed. The traditional FST measure, obtained from differences in allele frequencies between populations, has been used to identify CNVs loci subject to geographically varying selection. Here, we review advances and the application of multinomial-Dirichlet likelihood methods of inference for identifying genome regions that have been subject to natural selection with the FST estimates. The contents of presentation are not new; however, this review clarifies how the application of the methods to CNV data, which remains largely unexplored, is possible. A hierarchical Bayesian method, which is implemented via Markov Chain Monte Carlo, estimates locus-specific FST and can identify outlying CNVs loci with large values of FST. By applying this Bayesian method to the publicly available CNV data, we identified the CNV loci that show signals of natural selection, which may elucidate the genetic basis of human disease and diversity.
Introduction
It has become known that human genomes differ more as a consequence of structural variation than of single-base-pair differences [1-4]. Structural genomic variants, mainly in the form of copy number variants (CNVs), have recently been rediscovered as contributors to evolution and as pathoetiologic elements for complex human diseases [5, 6]. However, so far, there are not many CNV-based genome-wide association studies or population genetics studies compared with the single-nucleotide polymorphism (SNP)-based counterparts. One notable CNV-based population genetics study was done by Jakobsson et al. [7]. They applied SNP, haplotype, and CNV information to reveal the structures of 29 world-wide populations. Even though their CNVs were not as effective as SNPs or haplotypes in discriminating those populations, the authors showed the potential to apply this information to human genetic studies. Other examples of CNV-based disease susceptibility studies are systemic autoimmunity diseases [8, 9], psoriasis [10], and human immunodeficiency virus (HIV) infection and progression to acquired immune deficiency syndrome (AIDS) [11]. Disease could affect the patterns of CNV diversity via natural selection, and higher copy numbers of the immunoregulatory and inflammatory cytokine gene CCL3L1, for example, are associated with lower risks of HIV infection and the progression to AIDS [11]; furthermore, in a genome-wide study, the level of population differentiation at this locus was found to be extraordinary compared to that of other CNVs, suggesting that natural selection may have influenced CCL3L1 copy number in humans [3].
The traditional FST measure is useful for identifying regions of the genome affected by natural selection. In a recently published review paper, Holsinger and Weir define Wright's F-statistics (FST in particular) [12] and describe methods-of-moment estimates and how FST estimates should be interpreted [13]. Although the authors also mention the maximum likelihood Bayesian estimates of FST, their description is very limited in identifying genomic regions under selection and do not present an application to the datasets. They simply compared locus-specific estimates of FST with its genome-wide distribution, and therefore, probabilities are not attached to those with a higher FST.
Here, we outline the steps that constitute testing for outlier loci in population datasets by the maximum likelihood Bayesian method, using BayeScan computer software [14] (Note that the terms of locus and CNV are used interchangeably in this paper). The logic for determining outlier loci is simple. If natural selection favors one allele over others at a particular locus in some populations, the FST at that locus will be larger than at loci in which among-population differences are purely a result of genetic drift. Therefore, genome scans that compare single-locus estimates of FST with the genome-wide background might identify regions of the genome that have been subjected to diversifying selection [15].
We will demonstrate FST estimation by maximum likelihood Bayesian method with the publicly available high-resolution CNV dataset generated by Conrad et al. [4]. We will also show that this method identifies several genomic regions showing signals of natural selection. Even though we focus mainly on the CNV data here, the detailed steps of analysis are analogous for other types of molecular marker data, such as microsatellites, SNPs, and amplified fragment-length polymorphisms.
Method-of-moment (or ANOVA) estimates of FST
F-statistics
Wright [12] introduced F-statistics (FST, FIT, and FIS) as a tool for describing the partitioning of genetic diversity within and among populations that are directly related to the rates of evolutionary processes, such as migration, mutation, and drift. Specifically, F-statistics can be defined in many different ways: in terms of variances of allele frequencies, correlations between random gametes, and probabilities that two gametes chosen have different alleles. Depending on the relativity to the subpopulation or to the total population, FST, FIT, and FIS are defined, where subscript IS refers to 'individuals within subpopulations,' ST to 'subpopulations within the total population,' and IT to 'individuals within the total population.'
Following the work of Cockerham [16], F-statistics are defined in terms of the variance components - that is, the total variation in the genetic data is broken down into three components: (a) between subpopulations within the total population (we sometimes say 'between populations'); (b) between individuals within subpopulations; and (c) between gametes within individuals. FST, FIT, and FIS are defined as the expectations under the model of a/(a + b + c), (a + b)/(a + b + c), and b/(b + c) and estimated by the corresponding sample values [17, 18]. Here, it is perhaps pertinent to mention that when Weir and Cockerham [18] presented these definitions, they assumed a model consisting of an ancestral population from which subpopulations have descended in isolation under the same evolutionary processes. Thus, it is meaningful to have a single measure of population structure; that is, a global FST, which is an average over subpopulations. However, in identifying candidate loci under natural selection, evidence for locus-specific selection is of interest, and thus the estimators of locus-specific FST will be described in the next section.
Often, readers may be confused with several terms appearing in population genetics. Wright [12] interprets FST as a measure of the progress of the subpopulation towards the fixation of one allele of each locus in the absence of mutation and hence called a 'fixation index.' FST is also interpreted as a measure of shared ancestry with the subpopulations, relative to that in the population, and is thus called the 'coancestry coefficient' [19]. Therefore, if the value of FST is small, it means that the allele frequencies within each subpopulation are similar; if it is large, it means that the allele frequencies of subpopulations are different. On the other hand, FIS or FIT is defined as the correlation between two gametes that form a zygote relative to the subpopulation or population, and thus, FIS (or FIT) is called the 'inbreeding coefficient' [19].
Estimating FST by ANOVA methods
The estimators of F-statistics proposed by Weir [17] and Weir and Cockerham [18] are based on an analysis of variance (ANOVA) of allele frequencies, equivalently called the method-of-moments estimates. The weighted ANOVA estimates of FST, FIT, and FIS may be expressed in terms of the mean sum of squares for gametes (MSG), individuals (MSI), and populations (we sometimes say 'between subpopulations') (MSP), where the mean squares are estimated by an ANOVA model. In estimating FST specifically for our analysis of CNV data, we need to consider unbalanced samples (i.e., populations of unequal size). However, as the formulas are messy, we present here those for balanced samples. Formulas for unbalanced samples can be found in Rousset (in Appendix A) [20].
The definition of F-statistics used here is
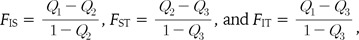
where Q values are probabilities of identity in state: Q1 among the genes (gametes) within individuals, Q2 among genes in different individuals within populations, and Q3 among the populations. The estimates 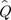 are expressed in terms of observed frequencies of identical pairs of genes in the sample, with the following relationships:
are expressed in terms of observed frequencies of identical pairs of genes in the sample, with the following relationships:

and
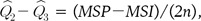
where n is the sample size of each population. Then, the single locus estimator  is given by
is given by
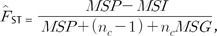
which is found in Weir (1997: 178) [17]. nc will be defined below. If one needs to obtain the multilocus estimator of  , it is usual to compute the estimator as a sum of locus-specific numerators over a sum of locus-specific denominators (see Weir [17] and Weir and Cockerham [18]). This is the case that map information for SNPs is obtained for each gene, and a weighted-average FST from all SNPs is estimated for each gene [18]. For a set of I loci, the multilocus ANOVA estimators are
, it is usual to compute the estimator as a sum of locus-specific numerators over a sum of locus-specific denominators (see Weir [17] and Weir and Cockerham [18]). This is the case that map information for SNPs is obtained for each gene, and a weighted-average FST from all SNPs is estimated for each gene [18]. For a set of I loci, the multilocus ANOVA estimators are

for nc = (S1-S2/S1)/(n-1), where S1 is the total sample size and S2 is the sum of squared sample sizes of populations [21]. For convenience, we denote the estimator  by FST.
by FST.
Rousset [21] explained that the multilocus estimators of Weir [17] and Weir and Cockerham [18] differ slightly, and these two also differ slightly from that proposed by Rousset [21], which assigns more weight to larger samples. In this paper, the GENEPOP software (version 3.4) (http://wbiomed.curtin.edu.au/genepop/) of Rousset was used for the calculation of FST. In order to distinguish from those of the method-of-moments estimates of Weir [17] and Weir and Cockerham [18], we will call the estimates of GENEPOP ANOVA estimates.
The estimated values of FST can be negative when levels of differentiation are close to zero and/or sample sizes are small, indicating no population differentiation at these loci [18]. One can assign a value of zero to negative FST estimates.
Identifying CNVs under Selection Using a Bayesian Method
Identifying selection
Identifying candidate CNVs under natural selection using locus-specific estimates of FST is of great interest, in view of our increased knowledge of the relationships among human populations from genome-wide patterns of variation. The logic for identifying selection is straightforward. The pattern of genetic differentiation at a neutral locus is completely determined by the demographic history, migration rates among the populations, and the mutation rates at the loci. It is reasonable to assume that all autosomal loci have experienced the same demographic history and migration rates among the populations, and the observed population structure can be largely explained by random drift at neutral loci. However, as the individuals from different populations often vary genetically at a few key sites in their genome, loci showing unusually large amounts of differentiation may indicate regions of the genome that have been subject to positive selection, whereas loci showing unusually small amounts of differentiation may indicate regions of the genome that have been subject to stabilizing (balancing) selection [15, 22-24]. Thus, the outlier method makes it possible to detect divergences in some loci of the genome due to selection.
Bayesian method
Balding and Nichols have proposed the use of population- and locus-specific estimates in the context of a migration-drift equilibrium model [24]. They modeled allele frequencies of biallelic markers using a beta distribution with expectation p and variance p(1-p)/(1+θ) so that FST = 1/(1+θ). Then, they used a likelihood-based approach to estimate population- and locus-specific FST.
This formulation was extended later to consider multiallelic loci [19]. Falush et al. [25] considered the nonequilibrium fission model that subpopulations evolve in isolation after splitting from an ancestral population. We will not distinguish the migration-drift equilibrium model and nonequilibrium fission model, since both lead to the same multinomial-Dirichlet distribution (or beta-binomial for biallelic loci) for the subpopulation allele frequencies [26]. The main difference between the two models resides in the interpretation given to FST: in the case of the migration-drift equilibrium model, FST measures how divergent each subpopulation is from the total population, while in the case of the fission model, it measures the degree of genetic differentiation between each descendant population and the ancestral population.
We consider a collection of J subpopulations and a set of I loci. Let Ki> be the number of alleles at the i th locus. The extent of differentiation between subpopulation j and the ancestral population at locus i is measured by 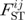 . Let pi = { pik } denote the allele frequencies of the ancestral population at locus i, where pik is the frequency of the allele k at locus i(
. Let pi = { pik } denote the allele frequencies of the ancestral population at locus i, where pik is the frequency of the allele k at locus i( = 1). We use p = { pi } to denote the entire set of allele frequencies of the ancestral population and
= 1). We use p = { pi } to denote the entire set of allele frequencies of the ancestral population and 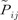 to denote the current allele frequencies at locus i for subpopulation j. Under the model and the definitions above, the allele frequencies at locus i in subpopulation j follow a Dirichlet distribution with parameters θjpi, a Bayesian prior distribution,
to denote the current allele frequencies at locus i for subpopulation j. Under the model and the definitions above, the allele frequencies at locus i in subpopulation j follow a Dirichlet distribution with parameters θjpi, a Bayesian prior distribution,
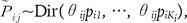
where θij = 1/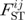 -1. The extent of differentiation at locus i between subpopulation j and the ancestral population is measured by
-1. The extent of differentiation at locus i between subpopulation j and the ancestral population is measured by 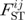 and is the result of its demographic history. The full prior distribution across loci and populations is given by
and is the result of its demographic history. The full prior distribution across loci and populations is given by
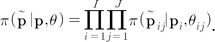
We need a hierarchical model for locus- and population-specific effects to identify candidate loci under natural selection. It is no doubt that population- and locus-specific estimates of 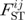 by the moments (or ANOVA) methods are likely to be inaccurate, especially for loci with a small number of different alleles. As an alternative, Beaumont and Balding [22] proposed a familiar logistic regression model to decompose population- and locus-specific
by the moments (or ANOVA) methods are likely to be inaccurate, especially for loci with a small number of different alleles. As an alternative, Beaumont and Balding [22] proposed a familiar logistic regression model to decompose population- and locus-specific 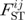 coefficients (bounded between 0 and 1) into a population-specific component, βj, shared by all loci and a locus-specific component, αi, shared by all populations [22]:
coefficients (bounded between 0 and 1) into a population-specific component, βj, shared by all loci and a locus-specific component, αi, shared by all populations [22]:
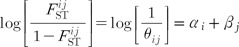
The locus-specific effects express mutation and some forms of selection, and population-specific effects express migration rates, population sizes, and population-specific mating patterns [22]. The advantage of this formulation is that instead of estimating locus- and population-specific I·J
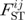 coefficients (as in the method of moments or ANOVA), we only have to estimate I the parameters αi and the J parameters βj. With the estimates of αi and βj,
coefficients (as in the method of moments or ANOVA), we only have to estimate I the parameters αi and the J parameters βj. With the estimates of αi and βj, 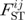 (and equivalently θij = exp(-(αi + βj)) can be estimated.
(and equivalently θij = exp(-(αi + βj)) can be estimated.
Above all, the estimate of αi is our objective to detect outlier loci as selection candidates. Departure from neutrality at a given locus is assumed when αi is significantly different from 0 at that locus. A positive value of αi suggests diversifying selection, whereas negative values suggest balancing selection. The posterior probability that a locus is subject to selection, P(αi ≠ 0), is estimated directly from the Markov Chain Monte Carlo method (MCMC) (see below).
Likelihood for allele counts
The data of codominant markers consist of allele counts obtained from samples of size nij. We use αijk to denote the number of alleles k observed at locus i in the sample from subpopulation j. Thus, nij = Σkαijk. The full dataset can be presented as a matrix N = { aij }, where aij = { αij1, αij2, ..., αijKi } is the allele count at locus i for subpopulation j. The observed allele frequencies, aij, can be considered as sampled from the true alleles frequencies 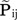 and therefore can be described by the multinomial distribution:
and therefore can be described by the multinomial distribution:
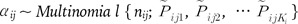
We adopt the multinomial-Dirichlet distribution as a marginal distribution of aij, the allele frequency counts at a locus within a subpopulation, and the reasons of its adoption are explained in Foll and Gaggiotti [26]:
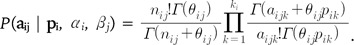
The joint likelihood for allele counts is obtained by multiplying across all loci and populations:
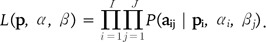
Since the allele frequencies in the ancestral population pi = { pik } are unknown, they are estimated by introducing a noninformative Dirichlet prior, pi ~ Dir (1, … , 1), into the Bayesian model [27].
The full Bayesian model is given by
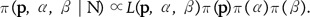
Following Beaumont and Balding [22], the Gaussian prior distributions are used for the population effects βj and for the locus effects αi. Their means and variances are chosen to improve convergence and for each 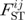 to have non-negligible density over almost the whole interval from 0 to 1.
to have non-negligible density over almost the whole interval from 0 to 1.
Identifying CNVs subject to selection
As described above, the effect of selection is parameterized by αi in the logistic regression. Thus, two models in the logistic, one that includes both effects of αi (i.e., αi ≠ 0) and βj (selection model, M2) and another one that does not include the effect of selection (i.e., αi = 0) and only includes the effect of βj (neutral model, M1), are considered.
We can decide in a Bayesian framework whether or not there is selection at all. This is done by estimating the posterior probabilities for two models for each locus in the logistic regression: neutral (M1) and selection (model 2, M2), on the basis of a dataset N = { aij }. We use a reversible jump MCMC algorithm [28] to estimate the posterior probability of each one of these models, and this is done separately for each locus i. We can then have posterior probability that a locus is subject to selection - that is, P(αi ≠0). This probability is estimated directly from the output of the MCMC by simply counting the number of times αi is included in the model (see Foll and Gaggiotti [27] for a more detailed explanation).
In BayeScan, selection decision (model choice decision), with a specific goal of detecting outlier loci in mind, is actually performed by using posterior odds (PO). For this, we first need to describe 'Bayes factors.' For the two models of neutral (M1) and selection (M2), the Bayes factor (BF) for model M2 is given by BF = P(N | M2)/P(N | M1), where N = { aij } is a dataset and P indicates probability. This BF provides a degree of evidence in favor of one model versus another. In the context of multiple testing - that is, testing a large number of loci simultaneously - we also need to incorporate our skepticism about the chance that each locus is under selection. This is done by setting the prior odds for the neutral model P(M1)/P(M2). We make selection decisions by using PO, which is defined as PO = P(M2|N)/P(M1|N) = BF × P(M2)/P(M1). PO are simply the ratio of posterior probabilities and indicate how much more likely the model with selection (M2) is compared to the neutral model (M1) (GENEPOP software). PO of 0.5-1.0, 1.0-1.5, 1.5-2.0, and 2-∞ are, respectively, considered as substantial, strong, very strong, and decisive evidence for selection [14].
A big advantage of posterior probabilities is that they directly allow the control of the false discovery rate (FDR), where FDR is defined as the expected proportion of false positives among outlier loci. Controlling for FDR has a much greater power than controlling for family-wise error rates using Bonferroni correction, for example [29]. In BayeScan, by first setting a target FDR, the PO threshold achieving this FDR is determined, and outliers equal to or above this PO threshold are listed in the output of R that is provided along with BayeScan.
Empirical Distribution of FST Based on CNV
Study populations
We obtained the high-resolution CNV data by Conrad et al. [4] from the Database of Genomic Variants (http://projects.tcag.ca/variation/). The dataset consists of 90 Han Chinese (CHB) and Japanese (JPT), 180 Caucasians of European descent (CEU), and 180 Yoruba (YRI) samples. Among the 450 individuals, we removed 19 individuals with more than 400 missing CNV genotypes. Each CNV was analyzed as biallelic dominant data, classified as neutral versus non-neutral (losses or gains).
Empirical distribution of FST
To assess population differentiation with an allele frequency spectrum of CNVs, the locus-specific estimates by ANOVA method and by hierarchical Bayesian method were obtained from all autosomes. The estimated values by the ANOVA method (moments estimates) can be negative when levels of differentiation are close to 0 and/or sample sizes are small, indicating no population differentiation at these loci [18]. In the hierarchical Bayesian method, the locus-specific estimate values are all positive, since they are generated by posterior distributions, which is an important benefit of a Bayesian method.
With the CNV data of this study, the summary statistics of FST was 0.0853 ± 0.1195 (median, 0.0360; range, -0.0071 to 0.8994) for the ANOVA method and 0.2459 ± 0.0115 (median, 0.2462; range, 0.2193 to 0.6166) for the Bayesian method. The empirical distributions of FST are found in Fig. 1. As can be seen from the Figure, low FST values are prevalent, and a large variability persisted in the ANOVA method, while FST distribution was sharply focused in the Bayesian method. The comparison of empirical distributions of the ANOVA and Bayesian methods demonstrates that Bayesian estimates perform better than ANOVA in identifying CNVs affected by natural selection.
Bayesian outlier detections
We searched the genome regions that show signals of natural selection by the Bayesian likelihood method implemented via reversible jump MCMC in BayeScan software [27]. For each CNV, BayeScan directly estimates the probability that a CNV is under positive selection, from which the PO are computed [27]. The posterior odds indicate how much more likely the model with selection is compared to the neutral model, and posterior odds of 5.0 was chosen as a threshold in the detection of CNVs under positive selection. This directly allows us to control the FDR, the expected proportion of false positives among outlier CNVs [29]. In our analysis, we chose FDR to be 0.05. In the BayeScan application, first following 10 pilot runs of 5,000 iterations and an additional burn-in of 50,000 iterations, we used 50,000 iterations (sample size of 5,000 and a thinning interval of 10).
Outliers detected by BayeScan
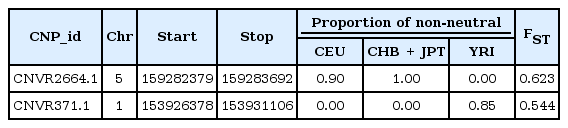
BayeScan identified the three outlier CNVs with Conrad et al.'s [4] CNV data (Table 1, Fig. 2). The most decisive outlier is CNVR2664.1 (chromosome 5), in which most CEU (90%) and all CHB + JPT populations are outlying gain or loss status. The next decisive outlier is CNVR371.1 (chr. 1), in which only the YRI population has non-neutral CNVs.
Conclusion
In general, the observed population structure observed by hierarchical clustering, multidimensional scaling (MDS) plots, and tree plots can be largely explained by random drift at neutral CNVs. However, as individuals from different populations often vary genetically at a few key sites in their genome, only the outlier method makes it possible to detect accelerated divergence in some CNV regions of the genome due to local selection. This local selection is detected relative to the majority of CNVs, in which among-population differences are purely a result of genetic drift.
Successful outlier detection depends on reliable and obtainable estimates of FST and also on sampling variances of FST. Very large variances that are associated with single locus moment estimates of FST preclude the use of these estimates to detect selection in spite of the fact that sampling variances will decrease with the number of alleles at a locus and with the numbers of populations sampled. In this respect, the availability of locus- and population-specific Bayesian estimates of FST provides a set of tools for identifying genomic regions or populations with unusual evolutionary histories. The most important benefits of Bayesian estimates and its selection method are that the Bayesian methods allow probability statements to be made about FST and can be extended to explore the relationship with demographic or environmental covariates in the model [26]. Furthermore, likelihood-based Bayesian methods have the flexibility to accommodate missing data. However, implementations of Bayesian methods may be computationally demanding.
Selection provides information about the adaptation to a wide range of habitats and climates [30], and thus, interpreting the story of human adaptation is an interesting research area for the studies of evolution and disease processes in the future. Thus, more studies of outlier detection need to be replicated with large population-based data.
Acknowledgments
This study was supported by a grant from the Korea Healthcare Technology R&D Project (A092258), Ministry of Health and Welfare, Republic of Korea.