Efficient Mining of Interesting Patterns in Large Biological Sequences
Article information
Abstract
Pattern discovery in biological sequences (e.g., DNA sequences) is one of the most challenging tasks in computational biology and bioinformatics. So far, in most approaches, the number of occurrences is a major measure of determining whether a pattern is interesting or not. In computational biology, however, a pattern that is not frequent may still be considered very informative if its actual support frequency exceeds the prior expectation by a large margin. In this paper, we propose a new interesting measure that can provide meaningful biological information. We also propose an efficient index-based method for mining such interesting patterns. Experimental results show that our approach can find interesting patterns within an acceptable computation time.
Introduction
Biological sequences, such as DNA sequences, have a great number of contiguous patterns consisting of frequent items. Which patterns are interesting to biologists? Is a pattern that occurs more frequently more interesting? So far, in most approaches, the number of occurrences has been a major measure of determining an interesting pattern. This measure, however, is not enough to discriminate a pattern from the background noise and may induce much time to spend for checking patterns of no biological meaning. Researchers are more interested in contiguous patterns that are statistically significant than those simply occurring frequently. The aim of mining interesting patterns is to analyze the important biological functions hidden in the extremely large amounts of genomic sequences. In this work, we aimed to discover surprising contiguous patterns that occur at a frequency higher than their expected frequencies. To find such surprising patterns with confidence, we chose to use a more suitable measure, information [1], which is widely studied and used in the field of communication. In information theory, if a pattern is expected to occur frequently based on some prior knowledge or by chance, then an occurrence of that pattern carries less information. Thus, we can use information to test the surprise of an occurrence of a pattern. The information gain is introduced to denote the accumulated information of a pattern in a DNA sequence and is used to exhibit the degree of surprise of the pattern.
Many works for sequential pattern mining take an a priori approach, such as Agrawal and Srikant [2], who used downward closure property to prune infrequent patterns, which says that if a pattern is infrequent, all of its superpatterns must be infrequent. It suffers from the level-wise difficulty for candidate generation-and-test and needs several database scans for sequential pattern mining. A typical Apriori-like approach such as Generalized Sequential Patterns (GSP) [3] is a good example of this category. An efficient algorithm, PrefixSpan [4], has been proposed, representing projection-based sequential pattern mining. This approach examines only the prefix subsequences and projects only their corresponding postfix subsequences into the databases. Sequential patterns are grown by exploring length-1 frequent patterns in each projected database. Using the projected database, however, every expansion of sequential patterns needs a recursive process, which is not effective for DNA sequence mining. The problem of finding the frequent maximal contiguous pattern from sequences more than two has been introduced in [5-8]. In addition, Yang et al. [9] have proposed an interesting technique to find periodic patterns in a sequence of events. Lu et al. [10] have proposed a pattern discovery algorithm that can identify over-represented patterns inside DNA sequences by introducing a new measurement system.
Another efficient algorithm, MacosVSpan [11], has been proposed, which gets the maximal subsequence of each data item by fixed-length spanning and finally looks for frequent maximal contiguous patterns using a suffix tree. Although this approach reduces recursive execution for expanding sequence patterns, it also suffers from the problem of producing and using projected databases. For long data sequences, the projected database grows much faster in comparison with the original database. Kang et al. [12] have proposed an approach to improve MacosVSpan using a fixed-length spanning tree, where each node maintains the frequency of subsequence overlapping. In this approach, all the candidates are produced first, including frequent and nonfrequent patterns; then, each candidate is scanned through the database to see whether it is frequent or not. This is obviously very time and memory-consuming.
Recently, Zerin et al. [13] proposed a position-based fast method to find contiguous frequent patterns, which needs to scan the database only once to construct the fixed length spanning tree. This approach builds the fixed length spanning tree in the same fashion as Kang et al. [12] but records the sequence identification (ID) and starting position of the fixed length pattern with the frequency in the leaf node of the tree, showing better results than the previous methods. Rashid et al. [14] have also proposed an efficient approach to mining significant contiguous frequent patterns from DNA sequences by constructing the fixed length spanning tree and by using a threshold that reduces the number of candidates. In this paper, we further develop this approach by proposing an index-based method, where the sequence ID and the staring position of each sequence are recorded in the leaf node of the tree as a variable length array. If a fixed-length pattern occurs multiple times in a sequence, we put the sequence ID as an index and put the start positions of the fixed length patterns in the variable length array. As a result, this approach significantly reduces memory space more than Zerin et al. [13].
Methods
Concepts and definitions
Let Σ = {A, C, G, T} be a set of DNA alphabets, where A, C, G, and T are called DNA characters or bases. A DNA sequence S is an ordered list of DNA alphabets. S is denoted by 〈c1, c2, ..., cl〉, where ci ∈ Σ and |S| denotes the length of sequence S. A sequence with length n is called an n-sequence. A sequence database D is a set of tuples 〈sid, S〉, where sid is a sequence ID. The sum of the lengths of all sequences in D is denoted as |D|=|S1|+|S2|...|Sn|
Definition 1 (Patter)
A pattern is a contiguous sub-sequence of DNA sequence S drawn from Σ = {A, C, G, T}. A sequence α = 〈a1, a2, ..., an〉 is called a contiguous sub-sequence of another sequence β = 〈b1, b2, ..., bm〉, and β is a contiguous super-sequence of α, denoted as α⊆β, if there exists integers 1 ≤ j1 ≤ j2 ≤ ... ≤ jn ≤ m and ji+1 = ji + 1 for 1 ≤ i ≤ n-1 such that a1 = bj1, a2 = bj2, ..., an = bjn. We can also say that α is contained by β. In our paper, we use the term "(sub)-sequence" to describe "contiguous (sub)-sequence" in brief.
Definition 2 (Support)
Given a pattern P and a sequence S, the number of occurrences of P in S is called the support of pattern P in sequence S, denoted as Sup(P, Si). For DNA sequence database D, the support of P in D is defined as 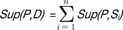 .
.
Definition 3 (Confidence)
Given a pattern P = P1, P2, ..., Pq and a DNA sequence database D, the confidence of P1P2 with respect to P1 is defined as Conf(P1P2, P1) = Sup(P1P2,D)/Sup(P1,D).
For example, the character "A" occurs 10 times and "AT" occurs 7 times, and in database D in Table 1, Conf(AT,A) = 7/10 = 0.7.
Definition 4 (Pattern probability)
Given a pattern P = P1, P2, ..., Pq (Pi is a DNA alphabet) and a DNA sequence database D, the pattern probability of P in D is defined as 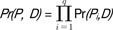 , where Pr(Pi, D) = # of occurrences of an alphabet Pi/|D|.
, where Pr(Pi, D) = # of occurrences of an alphabet Pi/|D|.
For example, the pattern probability of pattern "ATCG" in Table 1 is Pr(ATCG,D) = Pr(A,D) × Pr(T,D) × Pr(C,D) × Pr(G,D) = (10/55) × (18/55) × (12/55) × (15/55) = 0.182 × 0.372 × 0.218 × 0.273 = 0.00403.
Definition 5 (Information)
The information carried by a DNA character or base in DNA sequence database D is defined as I(c) = -log|C|Pr(c,D), where |C| is the number of distinct characters in D and Pr(c) is the probability of c occurs in D.
For example, the occurrence probability of character A in Table 1 is Pr(A,D) = # of occurence(A)/|D|. So, the probability of character A is Pr(A,D) = 10/55 = 0.182 in our example database. Then, the information of character A in D is, I(A) = -log|C|Pr(A,D) = -log4(0.182) = 1.228.
Definition 6 (Pattern information)
Given a pattern P = P1, P2, ..., Pq and a DNA sequence database D, the pattern information of P in D is defined as I(P) = -log|C|Pr(P,D) = I(P1) + I(P2) +......+ I(Pq).
For example, the pattern information of pattern "ATCG" is I(ATCG,D) = I(A,D) + I(T,D) + I(C,D) + I(G,D) = 1.228 + 0.713 + 1.098 + 0.9365 = 3.9755 in Table 1.
Definition 7 (Information gain)
Given a pattern P = P1, P2, ..., Pq and a DNA sequence database D, the pattern information gain of P in D is defined as IG(P) = I(P) × Support(P).
For example, the information gain of pattern "ATCG" is IG(ATCG,D) = 3.9755 * 5 = 19.8775 in Table 1.
Definition 8 (Finding interesting patterns)
Given a sequence database D and user-specified min_conf and min_in_gain, the problem of finding interesting patterns is to find the complete set of interesting patterns, such that IG(P) and Conf(P) are greater than min_in_gain and min_conf , respectively.
Surprising pattern-mining algorithm
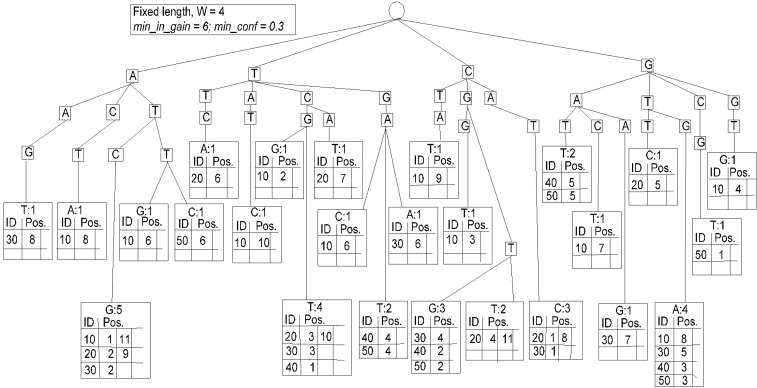
The method for mining surprising contiguous patterns from a DNA sequence database proceeds as follows. For constructing the fixed length spanning tree, we follow the method suggested by Kang et al. [12] - that is, read the database sequences and, starting from the first of each sequence, move the position one by one of the fixed length window throughout the sequence (Fig. 1). We put the sequence ID and the starting position in the leaf node of the tree as a variable length array, in addition to the frequency of the pattern moving of the window.
Fig. 2 shows our proposed algorithm. It has two steps. The first step recursively scans the subsequence with the same length as the fixed-length window from the given sequences to construct a fixed-length spanning tree and put the database sequence ID and starting position of the pattern in the leaf node of tree as a one-side open variable length array. At this time, it calculates the character probabilities for A, C, G, and T, respectively. It is straightforward for the calculation of character probabilities for A, C, G, and T. By adding all occurrences of A, C, G, and T and dividing by the total number of characters in the database, it can be obtained easily. After calculating character probabilities, we can calculate character information, pattern information, and pattern information gain by using definition 5, definition 6, and definition 7.
The second step generates fixed-length patterns from the constructed spanning tree with satisfying the minimum information gain threshold and minimum confidence threshold, and expands sequences by joining candidates and checking the frequency and starting position of the candidates. At the time of joining the sequences with the same length to generate the candidates of the next length, it checks whether the second candidate starts right to the next position of the first one with the same ID or not. If so, it increases the frequency counter by one. Finally, it checks the minimum information gain and minimum confidence threshold. If the pattern satisfies both thresholds, then it is added to the next-length candidate pattern. This process is recursively followed for all the candidates with the same length to generate the next-length surprising candidates.
The spanning tree is shown in Fig. 3, which is constructed based on the database available in Table 1. We have constructed a fixed-length spanning tree using the method suggested by Zerin et al. [13] but put the sequence ID and the staring position in the leaf node of the tree as a variable length array. Once the tree is constructed like Fig. 3, retrieval of the tree can obtain contiguous subsequences with length-4, satisfying the satisfying minimum information gain threshold and minimum confidence threshold. Then, the obtained length-4 surprising contiguous patterns are 〈ATCG〉, 〈TCGT〉, 〈TGAT〉, 〈CGTG〉, 〈CGTT〉, 〈CATC〉, and 〈GTGA〉, shown in Fig. 4.
To generate the length-5 surprising contiguous patterns, we need to join the length-4 surprising patterns; all the items in the first pattern, excluding the first item, should be same as all the items of the second pattern, excluding the last item. The frequency counter of the next length pattern will increase if both of the patterns are present in the same sequence and the second pattern's starting positions are the right next to the position of the first pattern in the same sequence. If the generated patterns satisfy the min_in_gain and min_conf, we consider the new pattern as a next length surprising candidate. The obtained length-5 surprising patterns are 〈ATCGT〉, 〈TCGTG〉, 〈TCGTT〉, 〈CGTGA〉, 〈CATCG〉, and 〈GTGAT〉. From Fig. 2, we see pattern ATCG starts from the 1st and 11th positions of sequence 10, 2nd and 9th positions of sequence 20, and 2nd position of sequence 30.
The pattern TCGT starts from 3rd and 10th positions of sequence 20, 3rd position of sequence 30, and 1st position of sequence 40. As a result, the length-5 candidate ATCGT starts from the 2nd and 9th positions of sequence 20 and the 2nd position of sequence 30. So, the information gain of ATCGT is 14.065, and the confidence of ATCGT with respect to ATCG is 0.6, which satisfy both min_in_gain and min_conf thresholds.
Following the same process, the obtained length-6 surprising patterns are 〈CGTGAT〉, 〈CATCGT〉, and 〈TCGTGA〉, and the obtained length-7 surprising pattern is 〈TCGTGAT〉. Here, we scan the whole database only once to construct the fixed-length spanning tree and then never scan the database again. On the other hand, using an index-based method and min_in_gain and min_conf thresholds, our proposed approach consumes less memory and faster execution than Zerin et al. [13].
Results and Discussion
We compare the performance of the proposed approach with Zerin et al. [13] for searching contiguous subsequences. For this purpose, we use a randomly generated DNA sequence database and a real DNA sequence database. We first generated a DNA sequence database by means of C++ program that randomly generates the variable length datasets. This database contains 5,000 DNA sequences with lengths from 100 to 1,000. The real DNA sequence database is downloaded from the bio-mirror portal (http://www.bio-mirror.net), which contains 19,979 DNA sequences, with average sequence length 1,024. All programs are written in Microsoft Visual C++ 6.0 and run with the Windows XP operating system on a Pentium dual core 2.13 GHz CPU with 1 GB main memory.
In the first experiment, we compare the memory usage of our approach and Zerin et al. [13] by varying the sequence length. Fig. 5 shows the memory usage according to the sequence length change, where we used our generated database for construction of the spanning tree with a fixed length 7. Here, we used information gain threshold, min_in_gain = 35(%) and minimum confidence threshold, min_conf = 30(%). From this experiment, we can see that the proposed approach has efficient improvement over Zerin et al. [13]. When the sequence length becomes longer, it shows better performance in comparison with the existing algorithm.
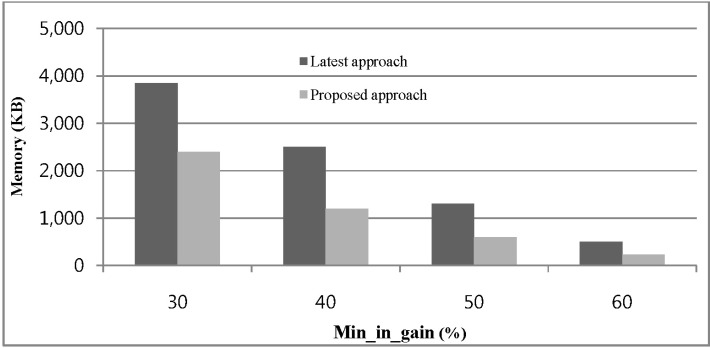
The memory consumption of our proposed approach and [13] for different values of min_in_gain over a real DNA sequence database is shown in Fig. 6. The x-axis in the graph indicates the change in min_in_gain as a percentage of the data point. A tree with a fixed length-10 was constructed using the aforementioned real datasets, and min_conf value 0.35 is taken. Fig. 6 indicates that for increasing the value of min_in_gain for both approaches, fewer candidates are generated and less memory is required.
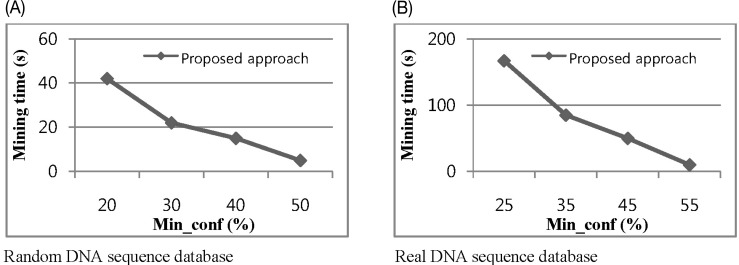
The second experiment examined mining time performance according to change in sequence length. Fig. 7A shows the mining time of the surprising contiguous patterns, starting from length-4 to length-9, in a randomly generated DNA sequence database, where we used information gain threshold min_in_gain = 35% and min_conf = 30%. On the other hand, we performed the same experiment with real DNA sequence datasets, where we used the value of min_in_gain = 45% and min_conf = 40%, which is shown in Fig. 7B. From Fig. 7, we can see that our proposed approach could mine the surprising contiguous patterns within a reasonable computation cost.
The third experiment shows the effect of information gain threshold on mining time to find out the surprising contiguous patterns up to length 8. In this experiment, we take min_conf 0.3 and 0.4 for the random and real datasets, respectively. Fig. 8 indicates that increasing the information gain threshold decreases mining time for both random and real datasets.
The fourth experiment studied the impacts of varying minimum confidence from 0.2 to 0.5 for random datasets and 0.25 to 0.55 for real datasets. This time, we take min_in_gain 0.3 and 0.4 for random and real datasets, respectively. Fig. 9 shows our proposed performance with different values for minimum confidence and illustrates a non-linear effect. The greatest change along the confidence axis is from 0.2 to 0.3 for random datasets and 0.25 to 0.35 real datasets. In most cases, the characters are evenly distributed. This means that the A, C, G, and T occur at almost the same ratio in the dataset as the frequency of each character, which is approximately 25%. So, if the min_conf is set to 0.3, most random patterns will be filtered out, and real patterns occurring more frequently than 25% of the time will survive and be extended.
To summarize, we have developed an index-based method, where we need to scan the database only once to mine the surprising contiguous patterns in biological data sequences, which are considered very important in bioinformatics and computational biology. Our aim is not to discover the patterns that occur often but rather to find patterns that are surprising by introducing a new threshold information gain. It has been shown by the experimental results that the proposed approach is very efficient in finding interesting patterns within a reasonable computation cost. For future work, we will try to optimize the proposed approach by considering a variety of environments with different parameters and also consider promoting new measurement parameters, which is very feasible for describing the sequences in a biological substance.
Acknowledgments
This work was supported by the National Research Foundation (NRF) grant (No. 2011-0018264) of the Ministry of Education, Science and Technology (MEST) of Korea.