 |
 |
- Search
| Genomics Inform > Volume 10(1); 2012 > Article |
Abstract
Mining interesting patterns from DNA sequences is one of the most challenging tasks in bioinformatics and computational biology. Maximal contiguous frequent patterns are preferable for expressing the function and structure of DNA sequences and hence can capture the common data characteristics among related sequences. Biologists are interested in finding frequent orderly arrangements of motifs that are responsible for similar expression of a group of genes. In order to reduce mining time and complexity, however, most existing sequence mining algorithms either focus on finding short DNA sequences or require explicit specification of sequence lengths in advance. The challenge is to find longer sequences without specifying sequence lengths in advance. In this paper, we propose an efficient approach to mining maximal contiguous frequent patterns from large DNA sequence datasets. The experimental results show that our proposed approach is memory-efficient and mines maximal contiguous frequent patterns within a reasonable time.
Mining patterns from DNA sequences refers to the task of discovering sequences that are similar or identical between different genomic locations or different genomes. How to efficiently discover long frequent contiguous sequences poses a great challenge for existing sequential pattern mining algorithms. The problem of finding the maximal contiguous frequent pattern is important in bioinformatics and has been used for predicting biological functions held in genomic sequences [1-4]. In the beginning, the problem of finding common subsequences from sequences of more than 2 was studied [1, 2]; then, many tried to solve more general sequential pattern mining problems.
A typical a priori algorithm, such as Generalized Sequential Pattern algorithm (GSP) [5, 6], adopts a multiple- pass, generation-and-test approach. In one pass, all single items (1-sequences) are counted. From the frequent items, a set of candidate 2-sequences are formed, and another pass is made to identify their frequency. The frequent 2-sequences are used to generate the candidate 3-sequences, and this process is repeated until no more frequent sequences are found. Normally, a hash tree-based search is employed for efficient support counting. Finally, non-maximal frequent sequences are removed. Based on this idea, a more efficient algorithm, called PrefixSpan [7], has been proposed, which examines only the prefix subsequences and projects only their corresponding postfix subsequences into the projected database (PDB). In each PDB, contiguous sequences are grown by exploring local length-1 frequent sequences. A memory-based pseudo-projection technique is developed to reduce the cost of projection and speed up processing. When mining long frequent concatenated sequences, however, this method becomes inefficient in terms of time and space. Therefore, it is impractical to apply PrefixSpan to mine long contiguous sequences, like biological datasets.
Pan et al. [8] proposed to use a variable length spanning tree to mine maximal concatenated frequent subsequences and developed algorithms, called MacosFSpan and MacosVSpan, based on the PrefixSpan approach. MacosVSpan is efficient for mining long concatenated frequent sub-sequences, whereas MacosFSpan has some limitations, because it constructs length-4 fixed length candidate sequences first and recursively mines length-5, length-6 candidate sequences, etc. This is very time consuming, because in a practical DNA sequence database, a sub-sequence may occur multiple times in the same sequence. Another problem is that both MacosVSpan and MacosFSpan use the pointer-offset pair to represent the suffixes inside the in-memory pseudo PDB, which is not enough to represent the huge number of suffixes in a physical PDB. Kang et al. [9] have claimed that their algorithm is more efficient than the MacosVSpan algorithm, but it was based on MacosFSpan, which needed multiple scans of the database. Recently, Zerin et al. [10] have proposed an indexed-based method to find the frequent contiguous sequences with single database scanning. This approach builds the fixed-length spanning tree in a way similar to Kang et al. [9], but it records the sequence IDs and starting position of the fixed length patterns with frequency in the leaf node of the tree. Although this approach shows better results than its predecessors in terms of space, time complexity is still not acceptable.
A practical DNA sequence database contains a large number of sequences, where a sub-sequence may occur multiple times in the same sequence. Therefore, we envisage using the concept of the suffix tree in terms of the variable length spanning tree of Pan et al. [8] to have the full advantages of prefix matching. Another aspect to consider is the size of real DNA sequence databases, which is ever increasing. For the cases where a DNA sequence database can not fit into the main memory, disk-based mining has been studied, based on partitioning [11-14]. Most of these techniques, however, only consider local frequency counting, although many frequent patterns may look infrequent due to local support pruning. In this paper, we propose a suffix tree-based approach for maximal contiguous frequent sub-sequence mining from DNA sequence datasets by means of a variable length spanning tree. We also introduce a combined main memory- and disk-based approach for mining maximal contiguous frequent patterns from extra large DNA sequence databases that can not fit into the main memory.
Let Σ = {A, C, G, T} be a set of DNA alphabets, where A, C, G, and T are called DNA characters or four bases; A is for adenine, C for cytosine, G for guanine, and T for thiamine. A DNA sequence S is an ordered list of DNA alphabets. S is denoted by 〈c1, c2... cl〉 where ci ∈ Σ and |S| denotes the length of sequence S. A sequence with length n is called an n-sequence. DNA sequence database D is a set of tuples 〈Sid, S〉 where Sid is a sequence identifier and S is the corresponding sequence.
A sequence α = 〈a1, a2,..., an〉 is called a contiguous sub-sequence of another sequence β = 〈b1, b2, ..., bm〉, and β is a contiguous super-sequence of α, denoted as α⊆β, if there exists integers 1 ≤ j1 ≤ j2 ≤ ... ≤ jn ≤ m and ji+1 = ji + 1 for 1 ≤ i ≤ n-1 such that a1 = bj1, a2 = bj2, ..., an = bjn. We can also say that α is contained by β. In our paper, we use the term "(sub)-sequence" to describe a "contiguous (sub)-sequence" in brief. A contiguous frequent sub-sequence X is said to be maximal if none of its super-sequences Y is frequent.
Given a DNA sequence database D and a minimum support threshold δ, the problem of maximal contiguous frequent sub-sequence mining is to find the complete set of maximal contiguous frequent patterns from that database. For example, let our running DNA sequence database be D in Table 1, and the minimum support threshold δ ≥ 2. Sequence 〈ATCGTGACT〉 is 9-sequence since its length is 9. Sequence 〈ATCG〉 is a contiguous frequent sub-sequence because it is contained by sequences 10, 20, and 30. S = 〈CGTGATT〉 is a frequent contiguous sub-sequence of length 7 since both sequences 40 and 50 contain it. Moreover, it is one of the maximal frequent contiguous sub-sequences, because there is no contiguous frequent super-sequence of 〈CGTGATT〉 with a minimum support of 2.
Let a sequence S = (α + β); then, α is a prefix of S and β is called a projection of S w.r.t. prefix α.
Let α be a frequent contiguous sequence in a sequence database S. Then, α-PDB is the collection of postfixes of sequences in S, w.r.t. prefix α.
For the database in Table 1, for example, 〈C〉-PDB consists of eight postfix sub-sequences: 〈GTGACT〉, 〈T〉, 〈ATCGTT〉, 〈GTT〉, 〈ATCGTGAGA〉, 〈GTGAAG〉, 〈GTGATTG〉, and 〈GTGATT〉. We have the following lemma regarding the PDB for the mining of maximal contiguous frequent patterns.
Let D be a DNA sequence database such that α is prefix(s) of the sequences in the database. Considering the sub-sequence and super-sequence relationship in terms of contiguity, the size of α-PDB cannot exceed the size of D, which means |Dα| ≤ |D|.
The lemma is regarding the size of a projected database. Obviously, the α-PDB can have same suffix sequences as the original database D only if α appears in every sequence in D. Otherwise, if only those suffixes in D that are super-sequences of α will appear in the α-PDB, then α-PDB cannot contain more sequences than D. For every sequence γ in D such that γ is a super-sequence of α, γ appears in the α-PDB in whole only if α is a prefix of γ. Otherwise, only a sub-sequence of γ appears in the α-PDB. Therefore, the size of α-PDB cannot exceed the size of D.
For example, if we consider the 〈A〉-PDB from the example database, it contains 9 suffixes: TCGTGACT, CT, TCGATTG, TTG, TCGTGAGA, GA, TTG, TTACT, and CT. So, can we see that the suffixes CT, TTG, and GA sub-sequences among the suffixes. So, in terms of contiguity, TCGTGACT, TCGATTG, TCGTGAGA, and TTACT are the super-sequences. Therefore, 〈A〉-PDB contains only four suffixes. So, the size of the PDB cannot exceed the size of original database. This claims that any PDB created from a database that fits into the main memory will certainly be fitted into the main memory.
We describe our algorithm, called Maximal Contiguous Frequent Suffix tree algorithm (MCFS), to discover maximal contiguous frequent patterns from DNA sequence datasets. Let us assume for now that the DNA sequence database can be fit into the main memory. The method proceeds as follows: 1) construct four projected databases, namely 〈A〉, 〈T〉, 〈C〉, and 〈G〉, to mine contiguous frequent patterns; 2) insert the suffixes of PDBs into a suffix tree; 3) traverse the whole suffix tree and find the set of frequent contiguous patterns; 4) check the properties of maximality and find the set of maximal contiguous frequent patterns.
In order to efficiently discover frequent sub-sequences, we design a suffix tree structure that stores all the potential sub-sequences and their corresponding supports. A 'potential frequent sub-sequence' is a sub-sequence that has at least two matches with other suffixes inside the PDBs. Each PDB has its own corresponding sub-tree, defined as follows. The root of the tree is the entry point. Each node consists of three fields: item, support, and link to the next node. Item registers which item this node represents. Concatenation of all items along the path from the root to this node represents a sub-sequence. Support registers the support of this suffix sub-sequence from the root node to this node. This means that if we traverse a particular path from top to bottom, then the path from the root to this node represents a sub-sequence, and support of the last node in the path becomes the support of the sub-sequence. The height of the suffix tree is not fixed, because the lengths of the suffixes are variable.
Our proposed algorithm (Fig. 1) proceeds in three steps. The first step scans the original database and constructs four PDBs. While creating PDBs of A, T, C, and G, a register is maintained that checks for duplicate suffixes without sorting the suffixes. If a suffix appears more than once in a PDB, the suffix is inserted into a temporary buffer with support. If a suffix X has n replicas in α-PDBs, for example, we move X to the temporary buffer with support n. This kind of suffix uses very little space and thus can be stored in the memory. Then, we check the suffixes and merge the sub-sequence suffixes with super sequence suffixes according to lemma 1. In this way, the size of physical PDB does not exceed the size of the original database. Inside the PDBs, we do not register the value of sequence ID or offset, because we can directly insert suffixes into the suffix tree.
The second step creates and inserts suffixes into suffix tree. During the insertion process, four situations arise regarding the maximality problem. First, if the inserting sequence is contained by some suffixes in the PDBs, it will match a branch of the suffix tree; then, we delete it from the result set and increase support up to the matching point to stop inserting. Second, if the inserted sequence contains some sequence in the tree, denoted as α, one of its suffixes will match the branch representing α; then, we increase the support of α and delete it from the result set and continue to insert other suffixes. Third, if there exists a suffix totally matching a prefix, say α of a PDB, we continue to find the longest subsequence β following α in S, which matches a root-path in α-subtree. Fourth, if there exists a suffix α that partly matches a prefix, we merge it with the suffix and increase the corresponding support up to the matching point. Otherwise, we just insert it into the suffix tree as a new path. If a suffix has no matches with other suffixes inside a PDB, we just discard the suffix after the traversing.
The third step scans the suffix tree and finds the set of all maximal contiguous frequent patterns. It first finds the set of contiguous frequent sub-sequences and then finds the set of maximal contiguous frequent patterns by checking the properties of maximality.
Let us demonstrate the MCFS algorithm using the database of Table 1. 〈A〉-PDB contains only super-sequences of suffixes storing all sub-sequences physically. According to lemma 1, 〈A〉-PDB contains 4 suffixes: TCGTGACT, TCGATTG, TCGTGAGA, and TTACT. ACT and ATTG will be moved to 'frequent file' with their corresponding supports 2. The remaining three projected databases can be constructed in a similar manner (Table 2).
Now, the suffixes are inserted into the suffix tree. Fig. 2 shows the suffix sub-tree that can be traversed to find the set of contiguous frequent patterns. The figure illustrates the mining technique of maximal contiguous frequent patterns from A-subtree. Mining from T, C, and G-subtrees can be done in a similar way.
The traversal of the suffix sub-tree proceeds as follows. First, we visit the paths from root to every descending node, and we write the frequent contiguous sub-sequences in the frequent file. Table 3 shows the content of the frequent file with corresponding supports. The frequent file previously contained four frequent contiguous sub-sequences with their support, which are ATTG (2), ACT (2), CT (2), and GATTG (2). After the final traversal on the sub-trees, the contents of the frequent file will be updated. Now, we scan the 'frequent file' presented by Table 3 and check if the maximality criteria are met. Finally, we have five maximal contiguous frequent patterns written into the output file (Table 4).
When a DNA sequence database is too large (e.g., 100 GB or more) to fit into the memory, we have to store it on a disk. In this case, different mining techniques are needed, and partitioning is one such technique. Most disk-based partitioning techniques [11-14] find frequent patterns from each partition and check to discover all frequent patterns. This approach, however, has some drawbacks, because frequent patterns may look infrequent due to local support pruning. Suppose our database is partitioned into two parts, D1 and D2. Sequences 10, 20, and 30 are in D1, and 40 and 50 are in D2. Suffix ACT occurs once in D1, so it is not frequent. According to them [12, 13], we have to discard it for local support pruning. Another copy of ACT is in D2 (ID-50), so we discard it from the partition as well. If we consider globally, then ACT will be a frequent pattern, if the minimum support threshold is 2. In this way, many frequent patterns can be lost by partitioning.
In order to deal with this problem, we propose a technique using a combined approach of main memory and disk partitioning. During the first scanning over the database, we partition the original database residing in the disk into smaller parts so that each part can fit into the memory. In this process, the number of partitions should be minimized by reading as many DNA sequences into the memory as possible to constitute one partition. The set of frequent patterns in D is obtained by collecting the discovered patterns after running MCFS on these partitions. The actual maximal contiguous frequent patterns can be identified with only one extra database pass through support counting against all the data sequences in each partition, one at a time. Therefore, we can employ MCFS to mine databases of any size, with any minimum support, in just two passes of database scanning - one for the original database and one for the portioned databases. Firstly, store every frequent pattern into a temporary buffer storage, namely 'frequent file,' with their corresponding support, and infrequent patterns into temporary buffer storage, namely 'output file,' with their corresponding support as well. After that, we collect all the infrequent patterns from each partition and combine them to count the corresponding support of each infrequent pattern.
The main goal of this approach is to process one partition in the memory at a time to avoid multiple scans over D from the secondary storage. Fig. 3 indicates the technique of mining contiguous frequent patterns from disk-based extra large database. In the figure, D1, D2, ..., Dn are the partitions of the original database. Fi is the contiguous frequent patterns, and IFi is the infrequent contiguous patterns from each partition. CFP is contiguous frequent patterns, and MCFPi is maximal contiguous frequent patterns. Fi, IFi, CFP, and MCFPi are all stored on the disk.
We compare the performance of our MCFS algorithm with MacosVSpan for mining maximal contiguous frequent sub-sequences. In this comparison, we only consider the memory-based approach, as done by most existing works. All programs were written and compiled using Microsoft Visual C++ 6.0, run with Microsoft Windows XP with a Pentium Duel Core 2.13 GHz CPU with 4 GB of main memory and 500 GB hard disk. As for practical DNA sequence databases, 'Human genome' (Homo sapiens GRCh37.64 DNA Chromosome Part 1, 2, 3) and 'Bacteria DNA sequence dataset' were downloaded from the NCBI website (http://www.ncbi.nlm.nih.gov/nuccore/). The human genome database contains 112,000 sequences, with sequence length 60. The bacteria dataset consists of 20,000 sequences, with sequence length 1,040.
As for validating the combined memory-disk based approach, we aim to show only the run-time efficiency. We applied our main memory disk-based mining approach to Homo sapiens GRCh37.64 DNA Chromosome Part 1, 2, and 3. Part 2 has 98,000 sequences and a length of 60, and part 3 has 105,000 sequences with sequence length of 60.
With various values of minimum support, we compared the run-time performance of three approaches: MCFS (our algorithm), MacosVSpan [8], and Latest Approach [9]. Figs. 4 and 5 show the retrieval performance with respect to the change of minimum support, indicating that MCFS outperforms the other two.
We also compared the memory usage of the three approaches with various values of minimum support. The search space was relatively smaller, because we made use of sub-sequence and super-sequence relationships, and whenever reaching to the minimum support threshold, the sub-sequence for contiguous frequent patterns was not searched. Figs. 6 and 7 show the memory usage, indicating that our approach shows relatively low memory usage compared to the other two. Although both MacosVSpan and our MCFS algorithm process one PDB after another and then produce the maximal contiguous frequent patterns by traversing the suffix tree, the size of the PDB cannot be larger than the original database (according to our proposed lemma); hence, the PDBs can be fit in the memory. This is why MCFS consumes much less memory compared to MacosVSpan.
The Latest Approach [9] requires slightly larger memory, because it constructs the spanning tree by processing all of them at once. It does not consider the memory usage while creating and producing the fixed-length spanning tree. Since it first constructs the fixed-length spanning tree and then expands these candidate item sets to generate longer length candidate item sets, it is not guaranteed to be fit in the memory.
Finally, we validate our combined memory disk-based approach by applying it to Homo sapiens GRCh37.64 DNA Chromosome Parts 1, 2, and 3. We assume that Parts 1, 2, and 3 are partitioned and stored on the disk. With various settings of minimum support threshold, we measured the run-time performance (Fig. 8).
In this paper, we have proposed an efficient algorithm, called MCFS, for mining maximal contiguous frequent sub-sequences, which requires only one scan of the original DNA sequence database. The proposed algorithm has the following characteristics. First, it can accept any value of the minimum support threshold effectively by means of one-time database access and construction of a suffix tree. Second, it can effectively mine the complete set of maximal contiguous frequent patterns without specifying the sequence lengths in advance. Third, the proposed method can produce results only by tree search, without expansion for production of a candidate set. Fourth, from the experimental results, we can see the scalability of our approach. As a result, it can be applied not only to a DNA sequence with a small number of items (dimension) but also amino acid sequences with a large number of items whose sizes can be very large and other multi-dimensional sequence datasets. Our experiments show that MCFS outperforms other existing approaches for mining maximal contiguous sub-sequences. In the future, we intend to extend this work to include gaps and execute it on real biological datasets.
Acknowledgments
This work was supported by the National Research Foundation (NRF) grant (No. 2011-0018264) of the Ministry of Education, Science and Technology (MEST) of Korea.
References
1. Chvátal V, Sankoff D. Longest common subsequences of two random sequences. J Appl Probab 1975;12:306–315.

2. Hirschberg DS. Algorithms for the longest common subsequence problem. J Assoc Comput Mach 1977;24:664–675.

3. Huo H, Stojkovic V. A suffix tree construction algorithm for DNA sequences. In: Proceeding of IEEE International Conference on Bioinformatics and Bioengineering (BIBE'07), 2007 Oct 14-17; Boston, MA: pp 1178–1182.

4. Tata S, Hankins RA, Patel JM. Practical suffix tree construction. In: Proceeding of 30th International Conference on Very Large Data Bases (VLDB'04), 2004 Aug 29-Sep 3; Toronto: pp 36–47.

5. Agrawal R, Srikant R. Fast algorithms for mining association rules. In: Proceeding of 20th International Conference on Very Large Data Bases (VLDB'94), 1994 Sep 12-15; Santiago de Chile: pp 487–499.
6. Srikant R, Agrawal R. Mining sequential patterns: generalizations and performance improvements. In: Proceeding of 5th International Conference on Extending Database Technology (EDBT'96), 1996 Mar 25-29; Avignon: pp 3–17.

7. Pei J, Han J, Mortazavi-Asl B, Chen Q, Dayal U, Hsu MC. PrefixSpan: mining sequential patterns efficiently by prefix-projected pattern growth. In: Proceeding of IEEE International Conference on Data Engineering (ICDE'01), 2001 Apr 2-6; Heidelberg: pp 215–224.
8. Pan J, Wang P, Wang W, Shi B, Yang G. Efficient algorithms for mining maximal frequent concatenate sequences in biological datasets. In: Proceeding of 5th International Conference on Computer and Information Technology (CIT'05), 2005 Sep 21-23; Shanghai: pp 98–104.
9. Kang TH, Yoo JS, Kim HY. Mining frequent contiguous sequence patterns in biological sequences. In: Proceeding of 7th IEEE International Conference on Bioinformatics and Bioengineering (BIBE'08), 2008 Oct 8-10; Athens: pp 723–728.

10. Zerin SF, Ahmed CF, Tanbeer SK, Jeong BS. A fast indexed-based contiguous sequential pattern mining technique in biological data sequences. In: Proceeding of 2nd International Conference on Emerging Databases (EBD'10), 2010 Aug 30-31; Jeju.
11. Appice A, Ceci M, Turi A, Malerba D. A parallel, distributed algorithm for relational frequent pattern discovery from very large data sets. Intell Data Anal 2011;15:69–88.

12. Lin MY, Lee SY. Fast discovery of sequential patterns through memory indexing and database partitioning. J Inf Sci Eng 2005;21:109–128.
13. Nguyen SN, Orlowska ME. A further study in the data partitioning approach for frequent itemsets mining. In: Proceeding of 17th Australasian Database Conference (ADC'06), 2006 Jan 16-19; Hobart, Tasmania: pp 31–37.
Fig. 1
The MCFS algorithm. MCFS, Maximal Contiguous Frequent Suffix tree algorithm; PDB, projected database.

Fig. 3
Partitioning approach to discover maximal contiguous frequent patterns for extra-large databases. MCFS, Maximal Contiguous Frequent Suffix tree algorithm; MCFPi, maximal contiguous frequent patterns.

Fig. 4
Retrieval performance w.r.t. change of minimum support (Homo sapiens GRCh37.64 DNA Chromosome Part 1). MCFS, Maximal Contiguous Frequent Suffix tree algorithm.

Fig. 5
Retrieval performance w.r.t. change of minimum support (bacteria genome dataset). MCFS, Maximal Contiguous Frequent Suffix tree algorithm.

Fig. 6
Memory usage w.r.t. change of minimum support (Homo sapiens GRCh37.64 DNA Chromosome Part 1). MCFS, Maximal Contiguous Frequent Suffix tree algorithm.

Fig. 7
Memory usage w.r.t. change of minimum support (bacteria genome sequence). MCFS, Maximal Contiguous Frequent Suffix tree algorithm.
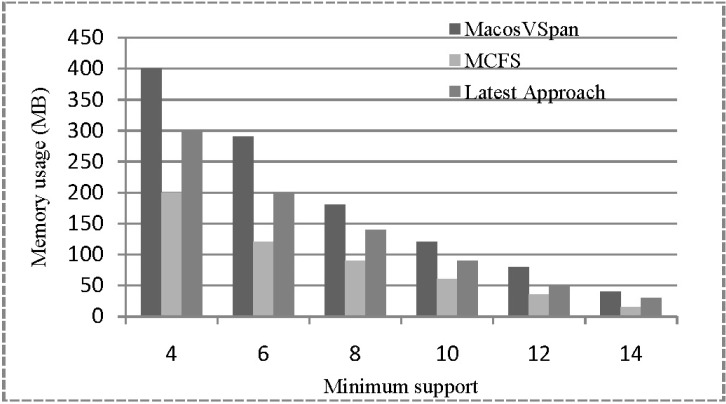
Fig. 8
Performance of MCFS algorithm w.r.t. increasing minimum support in partitioning approach (on Homo sapiens GRCh37.64 DNA Chromosome Part 1, 2, 3). MCFS, Maximal Contiguous Frequent Suffix tree algorithm.

Table 1.
A DNA sequence database
| Sid | Sequence |
|---|---|
| 10 | ATCGTGACT |
| 20 | CATCGATTG |
| 30 | CATCGTGAGA |
| 40 | TCGTGATTG |
| 50 | GCGTGATTACT |
Table 2.
Minimized physical projected databases (DBs)
| Projected DBs | Suffixes |
|---|---|
| <A> | TCGTGAGA, TCGTGACT, TCGATTG, TTACT |
| <T> | CGTGATTG, CGTGAGA, CGTGACT, GATTACT, CGATTG |
| <C> | ATCGTGAGA, GTGATTACT, ATCGATTG, GTACT, GTGATTG |
| <G> | CGTGATTACT, TGATTG, TGAGA, TGACT |
- TOOLS
-
METRICS

-
- 7 Crossref
- 7,560 View
- 50 Download
- Related articles in GNI
-
Efficient Mining of Interesting Patterns in Large Biological Sequences2012 March;10(1)






