|
 |
- Search
| Genomics Inform > Volume 16(4); 2018 > Article |
|
Abstract
Recently, there have been many studies in medicine related to genetic analysis. Many genetic studies have been performed to find genes associated with complex diseases. To find out how genes are related to disease, we need to understand not only the simple relationship of genotypes but also the way they are related to phenotype. Multi-block data, which is a summation form of variable sets, is used for enhancing the analysis of the relationships of different blocks. By identifying relationships through a multi-block data form, we can understand the association between the blocks in comprehending the correlation between them. Several statistical analysis methods have been developed to understand the relationship between multi-block data. In this paper, we will use generalized canonical correlation methodology to analyze multi-block data from the Korean Association Resource project, which has a combination of single nucleotide polymorphism blocks, phenotype blocks, and disease blocks.
Human diseases involve complex processes, including the interaction between multiple biological layers, including genetic, epigenetic, and transcriptional regulation [1]. For identifying genes involved in complex human diseases, genome-wide association studies (GWASs) are used by searching for single-nucleotide polymorphisms (SNPs) that occur more frequently in people without the disease. Prior GWASs identified SNPs related to several complex diseases, such as diabetes, heart abnormalities, and Parkinson disease. Researchers hope to find more SNPs associated with chronic diseases through GWASs in the future [2]. Most research has focused solely on the investigation of a single type of genomic data [3].
However, recent advances in genotyping technology have resulted in the large-scale generation of genomic data, and the variety of information collected has also become very diverse. Therefore, it has become very important to apply analytical methods that can fully utilize the given information. These data need to be analyzed in conjunction with disease variables, such as multiple SNPs and phenotypes. However, since these variables have different properties from each other, multi-block analysis that considers each property is necessary. Furthermore, even though these data have the potential to reveal great insights into the mechanism of disease and to discover novel biomarkers, statistical methods for integrative analysis of multi-block data are only emerging [4].
If there are only two variable blocks, canonical correlation analysis (CCA) can be applied. Research continues to try to analyze DNA-related data based on canonical analysis. Briki and Genest [5] adopted a canonical analysis approach to investigate correlated motions of atoms by molecular dynamics simulation. However, since there are more than two blocks in reality, the extended CCA methods that are applicable to more than two blocks have been less studied.
Hence, research has recently started to shift toward approaches using systematical models in order to integrate and analyze heterogeneous data comprehensively rather than through simple step-wise processes. Among multi-block analysis methods, generalized canonical correlation analysis (GCCA) is one of the most representative methods. Nevertheless, many studies have not yet been conducted on the application of multi-block methods to genomic data. Therefore, in the present study, we adopt GCCA to figure out the associations between SNP block, phenotype block, and disease block. We applied Korean Association Resource (KARE) data and analyzed the possibility and limitations of multi-block analysis methods for genomic data.
We focused on analyzing a multi-block dataset, considering the characteristics of each block. The multi-block dataset is a data type of horizontally concatenating more than two variable blocks. Usually, each block has different properties and forms and can also be partitioned by prior knowledge, but all blocks have the same number of observations. Suppose there are K blocks, and each block has pk number of variables (k = 1, ┬Ę┬Ę┬Ę, K). We can express the k-th block Xk as Xk = [x1, ┬Ę┬Ę┬Ę, xpk]. The total dataset X can be presented as [X1, ┬Ę┬Ę┬Ę, Xk, ┬Ę┬Ę┬Ę, XK].
As technology advances, this type of data is common in a variety of studies. For instance, in food science, blocks of variables could be physico-chemical measurements, sensory analysis data, and instrumental measurements [6]. Multiomics, the typical multi-block dataset in the medical field, means a new biological analysis approach where the datasets are multiple omics, such as the genome, proteome, transcriptome, epigenome, and microbiome [7ŌĆō9]. It usually focuses on associations between SNPs and traits, considering varying phenotypes.
Among various methods of dealing with a multi-block dataset, GCCA is used in this paper. Since it is extended from CCA, we start with an explanation of CCA. CCA is a method of inferring information from cross-covariance matrices. If there are two vectors X = (x1, ┬Ę┬Ę┬Ę, xn) and Y = (y1, ┬Ę┬Ę┬Ę, ym) of random variables and if there are correlations among the variables, the linear combinations of xi and yj to maximize the correlation with each otherŌĆötermed canonical variablesŌĆö are found through CCA [10].
GCCA is a way of extending CCA to adapt to more than two sets of random variables after removing dependencies within each set. The basic structure of CCA is to derive a new linear combination of the variables, called canonical variables, constituting each set and to estimate the correlation between canonical variables. In other words, canonical variables summarize the information inherent to the abbreviated set of multivariate data [11]. GCCA can be divided into two methods: using correlations and using covariance. In our paper, we use a method of analysis based on covariance. GCCA based on covariance uses the variance of ŌĆśblock scoresŌĆÖ to compute the residual matrices. For instance, in an Xk variable block, we can denote ak = (ak1 ak2 ┬Ę┬Ę┬Ę akpk)ŌĆ▓ as the coefficients for each variable in Xk block. Therefore, the canonical variables, yk (k = 1, ┬Ę┬Ę┬Ę, K), are expressed as:
The optimization problem is as follows.
The optimization problem tries to find coefficients of each block a1, a2, ┬Ę┬Ę┬Ę, aK that would maximize the weighted summation of the covariance of the two components. The cij in the equation implies the relationship between variable block Xi and Xj. If they have a relationship, we could assign cij = 1; otherwise, we could assign cij = 0. The function g() can be various functions, such as horst (g(x) = x), centroid (g(x) = |x|), and factorial (g(x) = x2). Among these methods, we applied horst methods. A design matrix C = (cjk) is pre-specified by the user to express the relationships between blocks. The element cjk is equal to 1 if block j and block k are connected and 0 otherwise [12, 13].
In this paper, we use data from the KARE project, which was initiated in 2007 to undertake a large-scale genome-wide association analysis among the 10,038 participants of two areas: Anseong and Ansan. It was established as part of the Korean Genome Epidemiology study (KoGES) in 2001, providing genomic and clinical variables for over 260 traits [14].
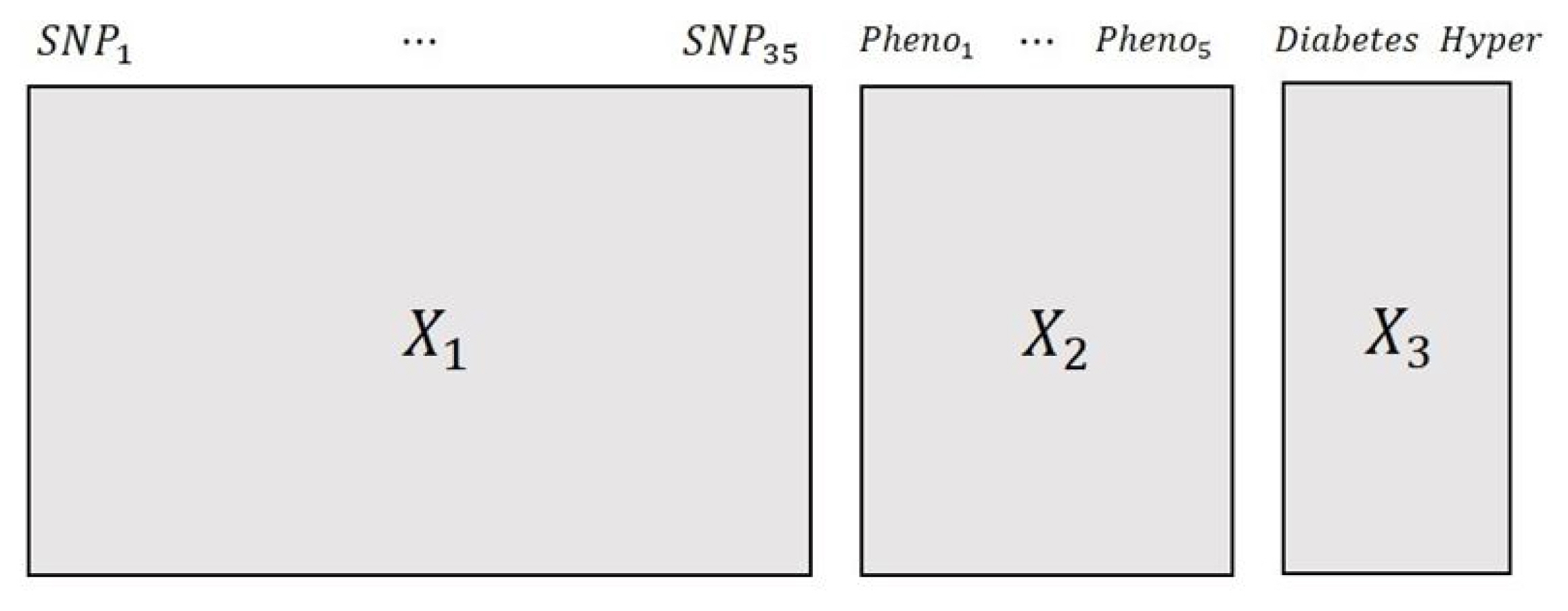
Among the KARE data, we decided to make three different variable blocks that included information on SNP variables, phenotype variables, and disease variables. Fig. 1 represents the multi-block form of the KARE data, which had three variable blocks, each with different characteristics. The first variable block, X1, is a block of SNP variables; the second variable block, X2, is a phenotype block that has five phenotype variables related to obesity. The last variable block, X3, is a disease block that has information on observational status in diabetes and hypertension.
The first variable block, X1, has information on 35 SNP variables, and each piece of data was recorded as 0, 1, or 2 according to their genotype. We extracted 35 SNP variables to be included in our analysis according to the specific following steps described in Fig. 2. The original KARE dataset has 311,779 variables, and we regarded 324 SNP variables as our main interest from the literature of Multi-QMDR analysis. The 324 SNP variables showed strong marginal effects in the univariate linear regression models in the paper [15]. From the 324 selected variables, we selected 47 variables that showed a significant relationship with our phenotype variables in the phenotype block. Lastly, we removed extremely similar SNP variables that had a correlation of more than 0.98 with each other in order to clearly see the correlation between variables.
The second variable block, X2, is a block of phenotype variables that have been proven to have a relationship with obesity. The five phenotype variablesŌĆōsuprailiac skinfold, subscapular skinfold, body mass index (BMI), waist-hip ratio, and waistŌĆōwere selected, and all of them are related to obesity. The third variable block, X3, is a block of diseases. Two disease variables were made from patientsŌĆÖ clinical traits. Participants whose ŌĆ£fasting blood glucoseŌĆØ was higher than 126, ŌĆ£blood glucose/oral glucose tolerance after 120 minutesŌĆØ was higher than 200, or ŌĆ£who had medication of diabetesŌĆØ were considered as having diabetes. Participants whose ŌĆ£subscapular skinfoldŌĆØ was over 140, ŌĆ£suprailiac skinfoldŌĆØ was over 90, or ŌĆ£who had medication of hypertensionŌĆØ were considered as having hypertension. Table 1 shows how each group was composed of according to our disease definition. Excluding individuals with missing values among the variables used in this process, the final sample size was 7,389 in the study.
Sex and age were considered as potential covariates which could affect our association analysis; for instance, coronary heart disease (CHD) is more common in men than in women. In addition, the risk of CHD increases with age in both sexes, but the increase is sharper in women [16]. Therefore, we divided the 7,389 observations into four groups based on a median age of 50 years and sex. Group 1 represents below the median age and males, while group 2 represents above the median age and males. Groups 3 and 4 represent females below and above the median age, respectively. For each group, our data were composed of three different blocks (J = 3)ŌĆōa gene data block, clinical data block, and disease status block. As with many multi-block genomic data, KARE data also have very different characteristics for each block. The gene data block has 35 SNP variables that are discrete and can only have values of 0, 1, or 2. The five phenotype variables of the clinical data block were continuous. The disease status block consisted of only two dummy variables, indicating the presence or absence of disease.
To check the association between blocks, logistic regression analysis was performed, and the coefficients and p-values are listed in Table 2. Table 2 shows the simple logistic regression of the variables in the phenotype and genotype blocks for diabetes and hypertension.
In Table 2, every variable in the phenotype block was statistically significant with diabetes, all with a p-value less than 0.001. However, in the regression with hypertension, the subscapular skinfold variable did not satisfy the significance level, which turned out to be a p-value of 0.578. Other than subscapular skinfold variable, all variables in the phenotype block showed significance of a relationship with hypertension. Therefore, there exists a relationship between each phenotype variable and two diseases, respectively. In contrast to the association between phenotype variables and disease variables, the association between SNP variables and disease variables were revealed only from certain genes. The genes related to diabetes were rs3856726, rs3782889, rs12229654, rs11066280, rs17092358, rs1378942, and rs11131794. The genes related to hypertension were rs221097, rs6965746, rs4472504, rs9939609, rs3782889, rs12229654, rs11066280, rs7136259, rs2254613, and rs1378942. There has been a study of SNPs associated with diabetes, in which the MYL2, C12orf51, and OAS1 genes were found to be significantly associated with 1-hPG, which has been understood as an additional risk factor for type 2 diabetes. Therefore, genes with rs3782889 (MYL2), rs12229654 (MYL2) were proven to have a valid relationship with diabetes [17].
The results of the GCCA were analyzed separately according to each group. In doing the GCCA, we needed to determine how many canonical variables we would have. The generalized canonical correlation results are presented in Table 3. Group 1 had generalized canonical correlations of 0.183, 0.156, and 0.095. The square of the generalized canonical correlations was 0.034, 0.024, and 0.009. The square of the generalized canonical correlation was used for calculating what proportion the canonical variable explains the dataset. For instance, the first canonical variable in group 1 had a square of the generalized canonical correlation value of 0.034 (rounded number is listed in Table 4). The proportion was calculated by using the square of the generalized canonical correlation. The first GCCA canonical variable explained 50.2% of the variation, while the second and third variables explained 36.4% and 13.4%, respectively. Therefore, for group 1, we used two canonical variables that were sufficient enough to represent the dataset. The other three groups also required two canonical variables to represent the dataset.
Since we have three blocks, we could make three initial canonical variables. The SNP blockŌĆÖs first canonical variable was U1 = a1SNP1 + ┬Ę┬Ę┬Ę + a35SNP35. The phenotype blockŌĆÖs first canonical variable was V1 = b1SUP + b2SUB + b3BMI + b4WHR + b5WAIST. The disease blockŌĆÖs first canonical variable was W1 = c1Diabete + c2Hyper. The term ai, bi, ci represents the coefficient of each i-th variable in the block. When we draw the first canonical variables U1 , V1 , W1 and the second variables U2, V2, W2, we can interpret the relationship of each blockŌĆÖs variable to the other block. In this paper, we first explain the relationship between blocks and then discuss the relationship within the blocks.
Once we conducted GCCA in SAS/IML, we could get information on the canonical variables and coefficients for each variable in the block. From the canonical variable value, we calculated the correlation between blocks, because the first and second canonical variables could represent most of the data. Table 3 represents the correlation between each blockŌĆÖs canonical variables. With a GCCA containing three blocks, the first correlation among three blocks is obviously high, but it can be different when we consider two pairs. The highest relationship was found in group 1, which had a correlation of 0.281 between the SNP blockŌĆÖs second canonical variable and the phenotype blockŌĆÖs second canonical variable. It is interesting that the relationship between the SNP block and phenotype block is the strongest, while the relationship between the SNP block and disease block is not that noticeable. This would imply a pathway relationship from SNP to disease, in which phenotype is the medium of the link between them. Another interesting point is the relationship between the first canonical variables is not that strong in the relationship between SNP and phenotype. Except group 4, the other three groups showed a stronger correlation between second canonical variables than first canonical variables. This is thought to be due to the fact that the phenotype spreads in the second axis.
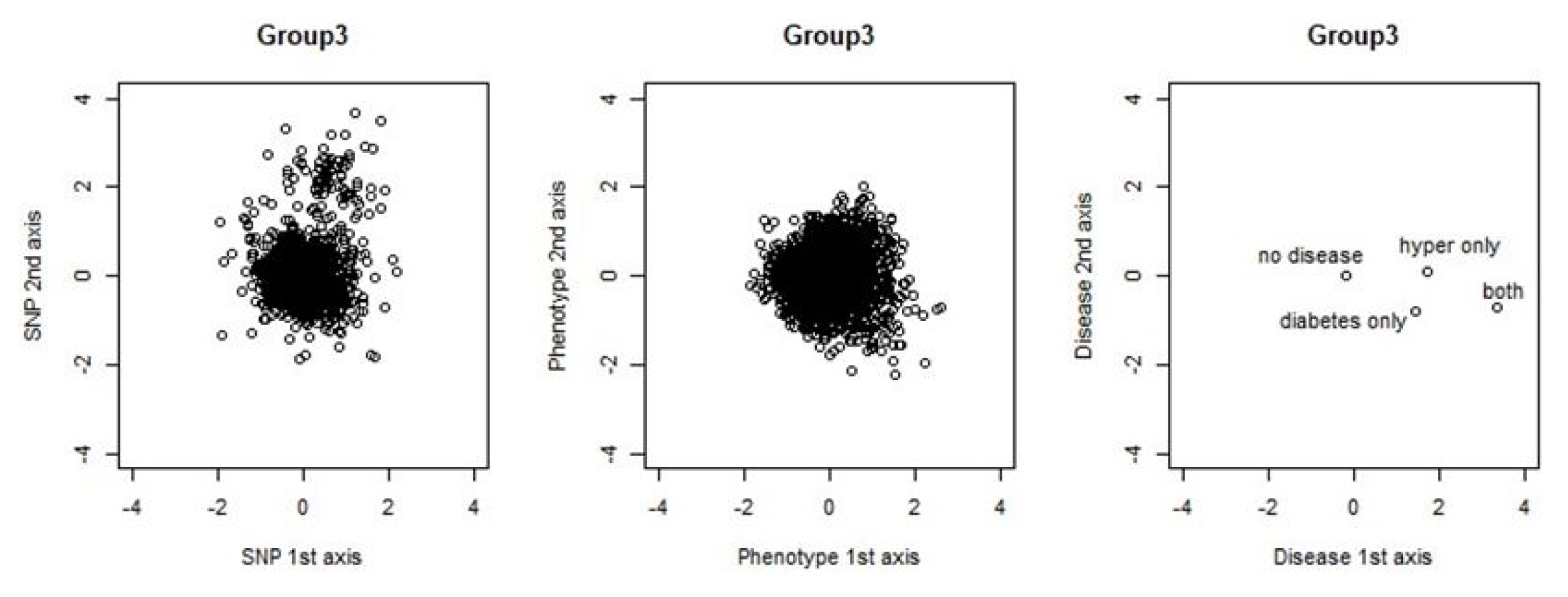
We also visualized the relation between blocks, particularly between the second canonical variables of the SNP and phenotype blocks. In Fig. 3, we illustrate a sample plot in group 3. The plot explains how the sample observation is located in each block by using the first and second canonical variable of each block. The SNP block appeared to be scattered compared with the other groups. The phenotype blockŌĆÖs observations are densely populated near the center (0,0), while the disease groupŌĆÖs observations only appear at four dots, since they are discrete data that have four possible disease cases. We can regard a sample that is located farther from center (0,0) is more influential for each SNP, phenotype, or disease block.
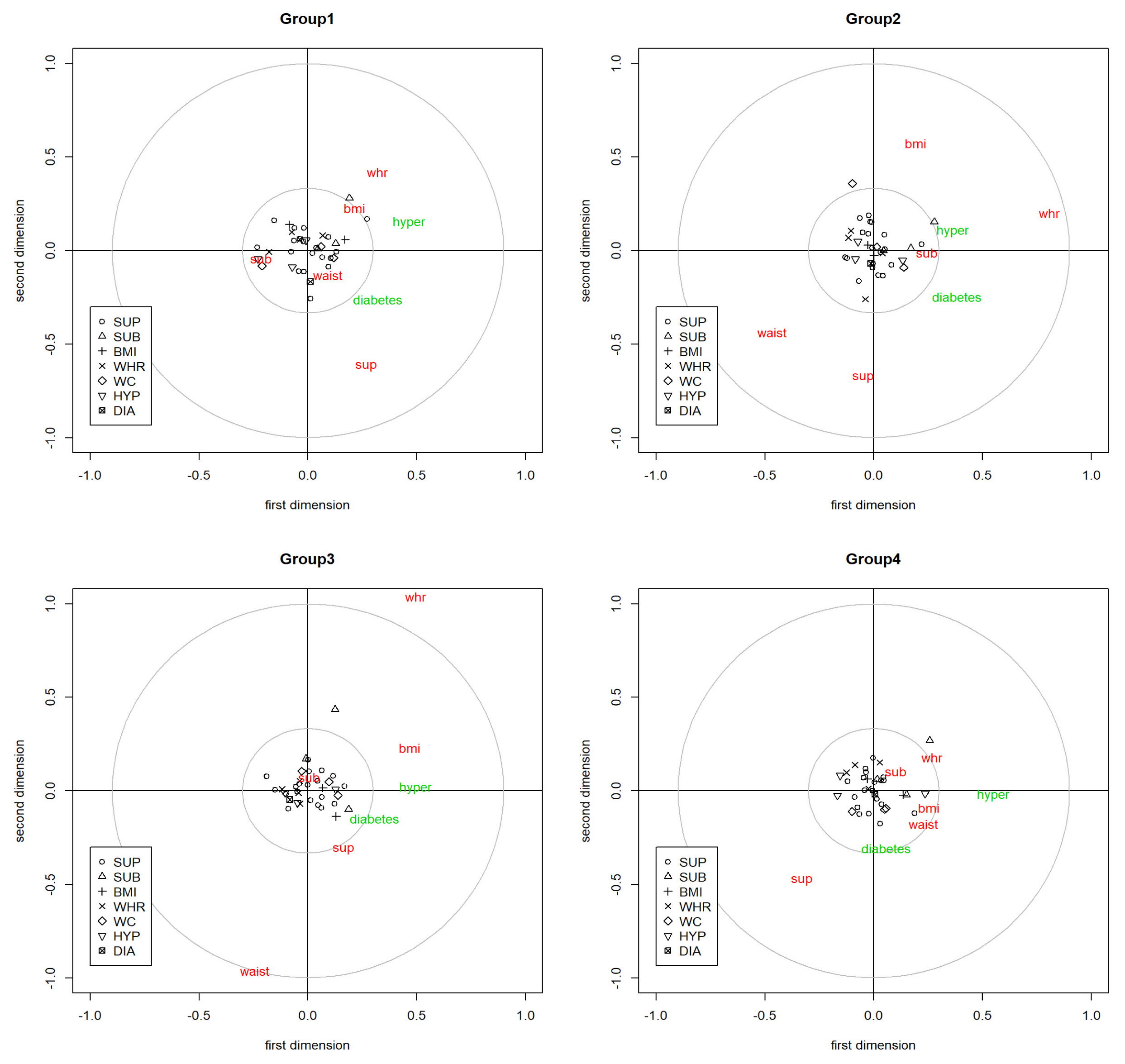
If we looked at each blockŌĆÖs variable plot, we can also understand how each variable in the block affects the canonical variable. The variable plot demonstrates how the variables are positioned within block; therefore, the goal is figuring out the internal relationship between variables. The x-axis is how much each variable influences the first canonical variable, and the y-axis is how much each variable influences the second canonical variable. In Fig. 4, there exist four variable plots, each representing how the variable in each block composes its block. The variables of the SNP block were represented as black points, which were categorized into seven different groups, based on where it is related the most.
We can interpret variable plots through making criteria for the x-axis and y-axis. If a variable exists farther away from the origin, the influence would be greater. We will illustrate group 1ŌĆÖs case in particular, while the interpretation of the other groups could be made, in addition to the first groupŌĆÖs interpretation. In group 1ŌĆÖs variable plot in Fig. 4, compared with the SNP variables, phenotype and disease variables showed more distinguishable features. The 35 SNP variables, which were presented as seven symbols according to their category in the graph, had a similar influence on SNP blocks. In the phenotype block, the variable waist-hip ratio and BMI had almost the same angle from the origin, whereas suprailiac skinfold (Sup) was almost in the opposite location in terms of the second components of the phenotype blocks. This means that waist-hip ratio and BMI gave similar traits compared with other phenotypes. When we considered the first-dimension axis, we could observe that subscapular skinfold (Sub) had a different trait from the other phenotype variables. In terms of disease blocks, we could separate people with disease and people without disease in terms of the x-axis, and hypertension and diabetes were also distinguishable with the y-axis criteria.
It is interesting for us to compare how the variable plot in each group was different. In terms of the SNP variable block, the rs527248 SNP variable had a triangular shape, which means the SNP is related to BMI the most compared with the association with other phenotype variables. Among SNP variables, rs527248, a point located outside of small gray circle in the first quadrant, had the most powerful influence on its canonical variable in all groups. In group 2, the influence of the rs527248 variable was more powerful on the first axis, whereas for groups 1, 3, and 4, there was much influence of the variable on the y-axis.
There are different aspects of the phenotype blockŌĆÖs variables from each group. In group 4, there existed extreme difference between the phenotype variables waist-hip ratio and waist. Whereas the waist-hip ratio variable was more than 1 on the y-axis, the waist variable was near ŌłÆ1, which is exactly the opposite location. If we look at the specific coordinates of the waist-hip ratio and waist variables, the influence of waist-hip ratio on the y-axis was 1.038, but the influence on the x-axis was 0.4966. In contrast, the waist variable in group 3 had a stronger influence on the y-axis than on the x-axis.
From our simple logistic regression, we had information that the SNP variable rs4472504 was related to hypertension disease, which had a p-value of 0.031. In our variable plot, the coordinates of rs4472504 were (ŌłÆ0.2113, ŌłÆ0.082), (ŌłÆ0.0987, 0.3589), (ŌłÆ0.028, 0.1049), and (ŌłÆ0.0995, ŌłÆ0.1101) in each group, respectively, whereas the coordinates of hypertension were (0.4645, 0.1513), (0.364, 0.1043), (0.4955, 0.0146), and (0.5504, ŌłÆ0.0219). Therefore, we cannot conclude that the relationship between a single SNP and a disease cannot be identical to the power of its influence on each axis.
In this paper, we have reviewed how to analyze multi-block datasetsŌĆöin particular, using Korean genomewide data: the KARE dataset. We conducted GCCA in order to compare the relationship between and within multi-blocks. To see the relationship between variables, we used SAS [18] to do GCCA and R to visualize the relationships between and within multi-block data in four different subgroups: group 1, group 2, group 3, and group 4. In the relationship between blocks, we could reveal that there existed a stronger association between second canonical variables than between first canonical variables. In addition, we found that the relationship between SNP block and Phenotype block was the strongest, whereas the relationship between SNP block and Disease block was not remarkable. To see the relationship within variables, we made plots that showed how much each variable contributed to the canonical variable. Some SNP variables showed distinguishable influence among variable blocks, but most SNP variables did not show big difference. Phenotype variables, however, were distinguished by each group and showed dramatic differences between groups. In this paper, GCCA was applied to the preselected SNP set which relied on previous literatures, however, further research could be started from screening SNPs which are associated with phenotype or disease status.
We had limitations, in that different types of data, including both discrete and continuous data, can lead to unsuccessful results in GCCA. However, the analysis regarding SNP, phenotype, and disease at the same time would be meaningful itself and can even be more productive when we add pathway assumption in the association analysis. Therefore, further research of this topic should focus on robust generalized canonical correlation analysis, which could function regardless of datatype, and on the relationship that we would like to specify.
Acknowledgments
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Science, ICT & Future Planning (NRF-2017R1A2B4011504).
Fig.┬Ā2
How to extract 35 single nucleotide polymorphism (SNP) variables. KARE, Korean Association Resource.
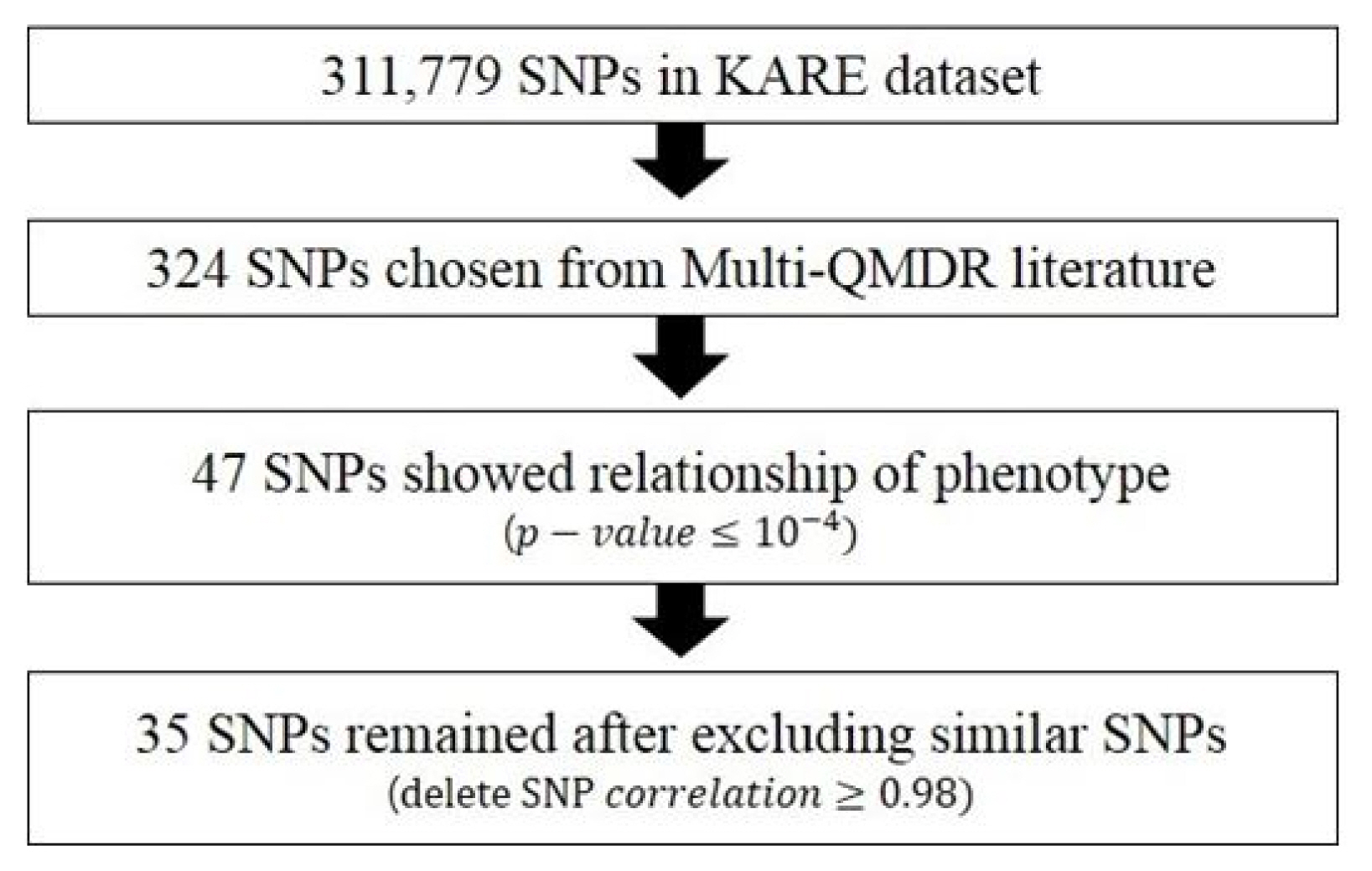
Fig.┬Ā4
Variable plot of each group. SUP, suprailiac skinfold; SUB, subscapular skinfold; BMI, body mass index; WHR, waist-hip ratio; WC, waist circumference; HYP, hypertension; DIA, diabetes.
Table┬Ā1
Disease frequency according to group
Table┬Ā2
Simple logistic regression coefficients for diseases
Table┬Ā3
Correlation between blocks
| Groupa | Canonical variable | SNPŌĆōPhenotype | SNPŌĆōDisease | PhenotypeŌĆōDisease |
|---|---|---|---|---|
| Group 1 | First-first | 0.204 | 0.164 | 0.180 |
| Second-second | 0.281 | 0.071 | 0.071 | |
|
|
||||
| Group 2 | First-first | 0.194 | 0.128 | 0.186 |
| Second-second | 0.277 | 0.085 | 0.034 | |
|
|
||||
| Group 3 | First-first | 0.169 | 0.102 | 0.250 |
| Second-second | 0.259 | 0.031 | 0.032 | |
|
|
||||
| Group 4 | First-first | 0.193 | 0.129 | 0.188 |
| Second-second | 0.192 | 0.061 | 0.069 | |
Table┬Ā4
Generalized canonical correlation results
| Groupa | Canonical variable | Generalized canonical correlation | Square of generalized canonical correlation | Proportion |
|---|---|---|---|---|
| Group 1 | 1 | 0.183 | 0.034 | 50.2 |
| 2 | 0.156 | 0.024 | 36.4 | |
| 3 | 0.095 | 0.009 | 13.4 | |
|
|
||||
| Group 2 | 1 | 0.171 | 0.029 | 46 |
| 2 | 0.151 | 0.023 | 35.8 | |
| 3 | 0.107 | 0.012 | 18.2 | |
|
|
||||
| Group 3 | 1 | 0.178 | 0.032 | 52.9 |
| 2 | 0.133 | 0.018 | 29.8 | |
| 3 | 0.101 | 0.010 | 17.3 | |
|
|
||||
| Group 4 | 1 | 0.171 | 0.029 | 55.9 |
| 2 | 0.115 | 0.013 | 25.2 | |
| 3 | 0.099 | 0.010 | 18.9 | |
References
1. Liu L, Li Y, Tollefsbol TO. Gene-environment interactions and epigenetic basis of human diseases. Curr Issues Mol Biol 2008;10:25ŌĆō36.


2. Tang CS, Ferreira MA. A gene-based test of association using canonical correlation analysis. Bioinformatics 2012;28:845ŌĆō850.



3. Kang M, Kim DC, Liu C, Gao J. Multiblock discriminant analysis for integrative genomic study. Biomed Res Int 2015;2015:783592.


4. Meng C, Zeleznik OA, Thallinger GG, Kuster B, Gholami AM, Culhane AC. Dimension reduction techniques for the integrative analysis of multi-omics data. Brief Bioinform 2016;17:628ŌĆō641.



5. Briki F, Genest D. Canonical analysis of correlated atomic motions in DNA from molecular dynamics simulation. Biophys Chem 1994;52:35ŌĆō43.


6. Eslami A, Qannari EM, Kohler A, Bougeard S. Multivariate analysis of multiblock and multigroup data. Chemometr Intell Lab Syst 2014;133:63ŌĆō69.

7. Bersanelli M, Mosca E, Remondini D, Giampieri E, Sala C, Castellani G, et al. Methods for the integration of multi-omics data: mathematical aspects. BMC Bioinformatics 2016;17(Suppl 2):15.



8. Bock C, Farlik M, Sheffield NC. Multi-omics of single cells: strategies and applications. Trends Biotechnol 2016;34:605ŌĆō608.



10. H├żrdle W, Simar L. Canonical correlation analysis. Applied Multivariate Statistical Analysis. (Johnson RA, Wichern DW, eds.). Berlin: Springer Berlin Heidelberg, 2003. pp. 361ŌĆō372.

11. Tenenhaus M, Tenenhaus A, Groenen PJ. Regularized generalized canonical correlation analysis. Psychometrika 2011;76:257ŌĆō284.

12. Tenenhaus A, Tenenhaus M. Regularized generalized canonical correlation analysis for multiblock or multigroup data analysis. Eur J Oper Res 2014;238:391ŌĆō403.

13. Tenenhaus M, Tenenhaus A, Groenen PJ. Regularized generalized canonical correlation analysis: a framework for sequential multiblock component methods. Psychometrika 2017;82:737ŌĆō777.


14. Cho YS, Go MJ, Kim YJ, Heo JY, Oh JH, Ban HJ, et al. A large-scale genome-wide association study of Asian populations uncovers genetic factors influencing eight quantitative traits. Nat Genet 2009;41:527ŌĆō534.



15. Yu W, Kwon MS, Park T. Multivariate quantitative multifactor dimensionality reduction for detecting gene-gene interactions. Hum Hered 2015;79:168ŌĆō181.


16. Jousilahti P, Vartiainen E, Tuomilehto J, Puska P. Sex, age, cardiovascular risk factors, and coronary heart disease: a prospective follow-up study of 14 786 middle-aged men and women in Finland. Circulation 1999;99:1165ŌĆō1172.


17. Go MJ, Hwang JY, Kim YJ, Hee Oh J, Kim YJ, Kwak SH, et al. New susceptibility loci in MYL2, C12orf51 and OAS1 associated with 1-h plasma glucose as predisposing risk factors for type 2 diabetes in the Korean population. J Hum Genet 2013;58:362ŌĆō365.



18. Huh MH. Quantification Analysis of Multivariate Data. Seoul: Freedom Academy, 1999. pp. 76ŌĆō86.
- TOOLS
-
METRICS

-
- 2 Crossref
- 0 Scopus
- 5,378 View
- 112 Download
- Related articles in GNI