EFMDR-Fast: An Application of Empirical Fuzzy Multifactor Dimensionality Reduction for Fast Execution

Sangseob Leem; Taesung Park

doi:10.5808/GI.2018.16.4.e37

Abstract

Gene-gene interaction is a key factor for explaining missing heritability. Many methods have been proposed to identify gene-gene interactions. Multifactor dimensionality reduction (MDR) is a well-known method for the detection of gene-gene interactions by reduction from genotypes of single-nucleotide polymorphism combinations to a binary variable with a value of high risk or low risk. This method has been widely expanded to own a specific objective. Among those expansions, fuzzy-MDR uses the fuzzy set theory for the membership of high risk or low risk and increases the detection rates of gene-gene interactions. Fuzzy-MDR is expanded by a maximum likelihood estimator as a new membership function in empirical fuzzy MDR (EFMDR). However, EFMDR is relatively slow, because it is implemented by R script language. Therefore, in this study, we implemented EFMDR using RCPP (c++ package) for faster executions. Our implementation for faster EFMDR, called EMMDR-Fast, is about 800 times faster than EFMDR written by R script only.

Keywords: EFMDR, Fuzzy-MDR, gene-gene interaction, multi-factor dimensionality reduction, RCPP

Introduction

In genome-wide association studies, many associations between single-nucleotide polymorphisms (SNPs) and phenotypes have been successfully discovered in many studies [1]. Despite the success of association studies, a large part of heritability remains unexplained as missing heritability [2]. Gene-gene interactions, rare variants, and structural variations are pointed to as causes of missing heritability.

For the detection of gene-gene interactions, the multifactor dimensionality reduction (MDR) method has been proposed by the reduction from genotype values of an SNP combination to a binary variable having a value of “high risk” or “low risk” [3]. This method has been widely expanded for specific objectives, such as balanced accuracy for imbalanced data [4], generalized MDR for covariate adjustments and continuous phenotypes [5] for survival phenotypes [6, 7], and odds ratio-based MDR [8], etc. [9–14].

Among MDR expansions, fuzzy-MDR uses the fuzzy set theory for an adaptation of membership function for reflecting the uncertainty of “high risk” or “low risk,” and detection rate increases have been verified in many simulations [15]. Fuzzy-MDR has been expanded for covariate adjustments and continuous phenotypes [16] and maximum likelihood estimator as the membership function as empirical fuzzy MDR (EFMDR) [17].

In EFMDR, a maximum likelihood estimator for each genotype is a membership value of ‘high risk’ or ‘low risk’ for the genotype. It has been proven that values of fuzzy balanced accuracy, based on maximum likelihood estimations, follow a chi-square distribution. Therefore, there is no need for cross-validation of p-value calculations. However, EFMDR is relatively slow, because it is implemented by R script only.

Methods and Results

To detect k-order interactions, MDR compares the balanced accuracy of all possible k-SNP combinations [3] and performs cross-validations. In fuzzy-MDR [15], fuzzy membership functions are used for reflecting the uncertainty of “high risk” or “low risk,” and validation of this uncertainty has been confirmed in various simulation experiments. In EFMDR [17], the maximum likelihood estimator of probabilities of “case” or “control” is used as the relative membership degree of “high risk” and “low risk,”. In addition, it is proven that the fuzzy balanced accuracy of EFMDR follows a chi-square distribution and that the cross-validation scheme is omitted by this property [17]. Because of the omission of cross-validation and the simple membership function, EFMDR is faster than fuzzy-MDR, but it is still slow in detecting high-order interactions.

For fast execution of EFMDR written in R, such optimization methods as using vector calculations might be a good approach. Instead, we used the RCPP package [18] for the implementation of faster EFMDR. In EFMDR, for detecting the k-locus interaction of a p-SNP dataset, (pk) SNP combinations are tested for the detection of an SNP combination with the highest fuzzy balanced accuracy. For example, for the detection of two-locus interactions in a 1000-SNP dataset, 1000*999/2=499,500 combinations are tested. This procedure—comparing fuzzy balanced accuracy values of all possible k-SNP combinations—dominates almost the total execution time. Therefore, we implemented a function for comparisons of balanced accuracy values of all possible k-SNP combinations using RCPP package (EFMDR-Fast).

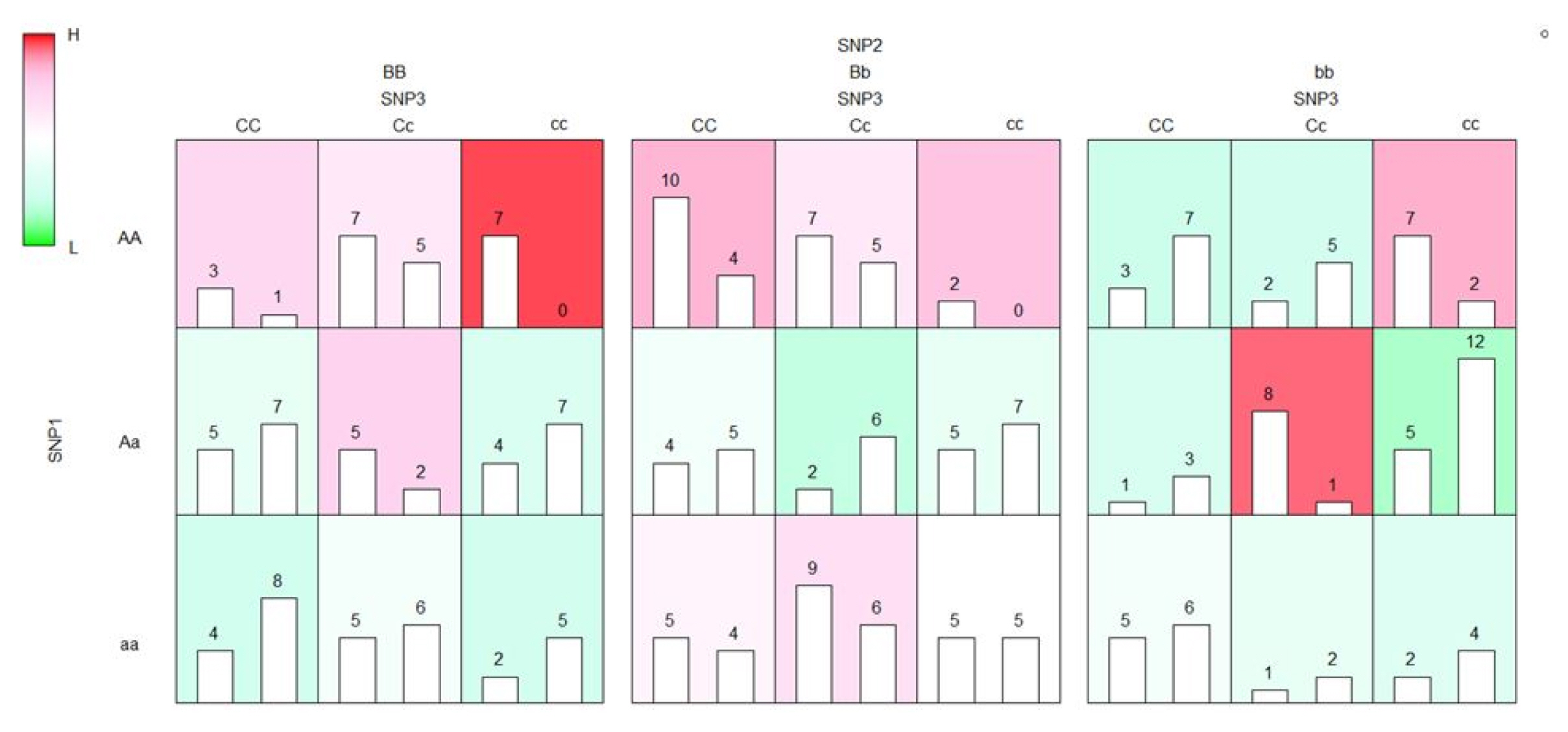
The results of the execution of EFMDR and EFMDR-Fast are in exactly the same formats. Hence, the results of EFMDR-Fast can be visualized easily using functions in EFMDR, as shown in Fig. 1.

We confirmed that the best SNP combinations of EFMDR and EFMDR-Fast are exactly the same. EFMDR-Fast is about 800 times faster than EFMDR. These comparisons were performed in R, version 3.5.1 on the Windows 10 platform with a 3.20 GHz CPU and 16 GB RAM. The program source codes and examples of EFMDR-Fast, written in R, and RCPP are available at http://statgen.snu.ac.kr/software/efmdr.

Acknowledgments

This work was supported by the Bio & Medical Technology Development Program of the National Research Foundation of Korea (NRF) grant (2013M3A9C4078158) and by grants of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (grant number: HI16C2037).

Notes

Availability: EFMDR-Fast is written in R and RCPP and is available at http://statgen.snu.ac.kr/software/efmdr.

Authors’ contribution

Conceptualization: SL, TP

Formal analysis: SL

Funding acquisition: TP

Methodology: SL, TP

Writing – original draft: SL, TP

Writing – review & editing: SL, TP

Conflicts of Interest

No potential conflict of interest relevant to this article was reported.

Fig. 1

Example of the visualization of the results of EFMDR-Fast. EFMDR, empirical fuzzy multifactor dimensionality reduction.

References

1. Welter D, MacArthur J, Morales J, Burdett T, Hall P, Junkins H, et al. The NHGRI GWAS Catalog, a curated resource of SNP-trait associations. Nucleic Acids Res 2014;42:D1001–D1006.

2. Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, et al. Finding the missing heritability of complex diseases. Nature 2009;461:747–753.

3. Ritchie MD, Hahn LW, Roodi N, Bailey LR, Dupont WD, Parl FF, et al. Multifactor-dimensionality reduction reveals high-order interactions among estrogen-metabolism genes in sporadic breast cancer. Am J Hum Genet 2001;69:138–147.

4. Velez DR, White BC, Motsinger AA, Bush WS, Ritchie MD, Williams SM, et al. A balanced accuracy function for epistasis modeling in imbalanced datasets using multifactor dimensionality reduction. Genet Epidemiol 2007;31:306–315.

5. Lou XY, Chen GB, Yan L, Ma JZ, Zhu J, Elston RC, et al. A generalized combinatorial approach for detecting gene-by-gene and gene-by-environment interactions with application to nicotine dependence. Am J Hum Genet 2007;80:1125–1137.

6. Gui J, Moore JH, Kelsey KT, Marsit CJ, Karagas MR, Andrew AS. A novel survival multifactor dimensionality reduction method for detecting gene-gene interactions with application to bladder cancer prognosis. Hum Genet 2011;129:101–110.

7. Lee S, Kwon MS, Oh JM, Park T. Gene-gene interaction analysis for the survival phenotype based on the Cox model. Bioinformatics 2012;28:i582–i588.

8. Chung Y, Lee SY, Elston RC, Park T. Odds ratio based multi-factor-dimensionality reduction method for detecting gene-gene interactions. Bioinformatics 2007;23:71–76.

9. Oh S, Lee J, Kwon MS, Weir B, Ha K, Park T. A novel method to identify high order gene-gene interactions in genome-wide association studies: gene-based MDR. BMC Bioinformatics 2012;13(Suppl 9):S5.

10. Huh I, Park T. Multifactor dimensionality reduction analysis of multiple binary traits for gene-gene interaction. Int J Data Min Bioinform 2016;14:293–304.

11. Kim Y, Park T. Robust gene-gene interaction analysis in genome wide association studies. PLoS One 2015;10:e0135016.

12. Yee J, Kwon MS, Park T, Park M. A modified entropy-based approach for identifying gene-gene interactions in case-control study. PLoS One 2013;8:e69321.

13. Lee SY, Chung Y, Elston RC, Kim Y, Park T. Log-linear model-based multifactor dimensionality reduction method to detect gene gene interactions. Bioinformatics 2007;23:2589–2595.

14. Yu W, Lee S, Park T. A unified model based multifactor dimensionality reduction framework for detecting gene-gene interactions. Bioinformatics 2016;32:i605–i610.

15. Jung HY, Leem S, Lee S, Park T. A novel fuzzy set based multi-factor dimensionality reduction method for detecting gene-gene interaction. Comput Biol Chem 2016;65:193–202.

16. Jung HY, Leem S, Park T. Fuzzy set-based generalized multi-factor dimensionality reduction analysis of gene-gene interactions. BMC Med Genomics 2018;11(Suppl 2):32.

17. Leem S, Park T. An empirical fuzzy multifactor dimensionality reduction method for detecting gene-gene interactions. BMC Genomics 2017;18(Suppl 2):115.

18. Eddelbuettel D, François R. Rcpp: Seamless R and C++ Integratio. J Stat Softw 2011;40:1–18.