 |
 |
- Search
| Genomics Inform > Volume 14(4); 2016 > Article |
Abstract
Many researchers have found that one of the most important characteristics of the structure of linkage disequilibrium is that the human genome can be divided into non-overlapping block partitions in which only a small number of haplotypes are observed. The location and distribution of haplotype blocks can be seen as a population property influenced by population genetic events such as selection, mutation, recombination and population structure. In this study, we investigate the effects of the density of markers relative to the full set of all polymorphisms in the region on the results of haplotype partitioning for five popular haplotype block partition methods: three methods in Haploview (confidence interval, four gamete test, and solid spine), MIG++ implemented in PLINK 1.9 and S-MIG++. We used several experimental datasets obtained by sampling subsets of single nucleotide polymorphism (SNP) markers of chromosome 22 region in the 1000 Genomes Project data and also the HapMap phase 3 data to compare the results of haplotype block partitions by five methods. With decreasing sampling ratio down to 20% of the original SNP markers, the total number of haplotype blocks decreases and the length of haplotype blocks increases for all algorithms. When we examined the marker-independence of the haplotype block locations constructed from the datasets of different density, the results using below 50% of the entire SNP markers were very different from the results using the entire SNP markers. We conclude that the haplotype block construction results should be used and interpreted carefully depending on the selection of markers and the purpose of the study.
Linkage disequilibrium (LD) means non-random association of alleles between different loci in a population [1]. Genetic variants in close proximity tend to be inherited together as a single haplotype and low frequency of recombination between them resulting in association between alleles of these variants in the population data [1,2]. Therefore, information of LD can provide evidences to support a hypothesis about population history and help to reveal genetic etiology [3,4]. Many researchers have studied the structure of LD patterns by observing population data and have found that one of the most obvious characteristics of the structure of LD is that the human genome can be divided into non-overlapping block partitions in which only a small number of haplotypes are observed [5]. These blocks are called haplotype blocks or LD blocks [6,7,8,9,10]. The variants within a same block tend to be in strong LD with each other whereas the variants across different blocks are mostly in weak LD or in linkage equilibrium [8].
The location and distribution of haplotype blocks can be seen as a population characteristic that is influenced by evolutionary phenomenon such as selection, mutation rate, recombination rate and population structure [11]. Especially, strong agreement between recombination hotspots and the haplotype block boundaries has been reported through comparisons of the block locations with the experimentally obtained locations of recombination hotpots [6]. In the other hand, an investigation on haplotype blocks using simulated data revealed that haplotype blocks can be formed without recombination hotspots [9]. However, their investigation in [9] used an operational definition for haplotype block in which all the single nucleotide polymorphisms (SNPs) are in strong LD with each other resulting in producing many short length blocks.
Several different methods for haplotype block partitioning have been developed and implemented in distributable software. Among them, Haploview carries three different methods for haplotype block partitioning each of which adopts a different operational definition for haplotype blocks: confidence interval (CI) method by Gabriel et al. [8], four gamete test (FGT) by Wang et al. [9], and solid spine (SS) method [10]. More recently, following the haplotype block definition of Gabriel et al. [8], some computationally efficient algorithms have been also released and these include MIG++ [12] and S-MIG++ [13]. MIG++ is also implemented in PLINK 1.9 with additional modification for computational efficiency [14].
Haplotype blocks can be directly obtained from the individual genetic association study data of SNP markers. Also, in many cases, they are identified using reference panel data such as HapMap or 1000 Genomes Project. These databases or study-specific data have different SNP marker sets with different density. If haplotype blocks are related to the biological causes such as recombination hotspots or population history, the location of blocks- the block boundariesŌĆöshould be markerŌĆöindependent and the most accurate estimation of haplotype block locations should be obtained from DNA sequencing data where every polymorphism is identified in the data. Therefore, to apply the haplotype block information obtained from the genotype data of a subset of polymorphisms in that region to the population genetic research or discovery of disease susceptibility variants, the effects of marker density on the haplotype block partition results should be carefully considered.
In this paper, we describe how the density of SNP markers affects haplotype blocks partitions by comparing the block partition results obtained from the experimental datasets sampled from the reference panel using several certain sampling ratio conditions. We also investigate how these effects of the marker density work differently for different haplotype block partitioning methods. The haplotype block partition methods we investigate include three methods implemented in Haploview (CI, FGT, and SS) [10], MIG++ implemented in PLINK version 1.9 [12,14], and S-MIG++ [13]. For reference panel to construct experimental datasets we use the 1000 Genomes Projects phase 1 release 3 dataset [15] and HapMap phase III dataset [16]. From our investigation, we found that low sampling ratio under 50% cannot guarantee marker-independent haplotype partition results for all methods and the haplotype blocks constructed from full density data tend to be divided into small length blocks compared to the results from low density data.
We compare the results of five haplotype block partition methods applied to the experimental datasets sampled from the 1000 Genomes Project dataset and the HapMap dataset with various marker density scenarios. The description of each haplotype block partition method follows.
The haplotype visualization software Haploview [10] implements three haplotype block partition methods, the CI method by Gabriel et al. [8], the FGT method by Wang et al. [9], and SS method [10].
In the CI method, the algorithm first classifies each pair of markers into one of three categories in terms of the LD measure DŌĆ▓ [3,17]: (1) ŌĆ£strong LDŌĆØ if the one-sided upper 95% confidence bound of DŌĆ▓ is >0.98 and the lower bound is >0.7, (2) ŌĆ£strong evidence for historical recombinationŌĆØ if the upper confidence bound of DŌĆ▓ is <0.9, (3) ŌĆ£non-informativeŌĆØ otherwise. The pairs satisfying the conditions (1) and (2) are said to be informative. Once all marker pairs are classified into three categories, a region is defined as a haplotype block if the outer-most marker pair (two markers at the starting and the ending position of the region) is in ŌĆ£strong LDŌĆØ and the proportion of the number of ŌĆ£strong LDŌĆØ marker pairs over the number of all informative marker pairs in the region is greater than 0.95. To partition a genomic region into an optimal set of haplotype blocks, the CI algorithm adopts a greedy approach: find the longest block region by examining the proportion of ŌĆ£strong LDŌĆØ marker pairs over all informative marker pairs located between each candidate outer-most marker pair in the remaining region at each iteration. In this way, the CI algorithm can add blocks which do not overlap with an already taken blocks.
The FGT algorithm begins by computing the population frequencies of the four possible two-marker haplotypes for each marker pair. By the FGT criterion, it regards that a recombination event has been occurred between two markers if all four possible two-marker haplotypes are observed with at least 1% frequency. Using this criterion, the algorithm constructs haplotype blocks of consecutive markers that do not show history of any recombination event between them.
The SS method defines the region as an LD blocks if the first and last markers in the region are in strong LD (DŌĆ▓>0.8) with all intermediate markers in the region. In the LD chart, the square matrix of a pairwise LD measure where the (i,j)-element represents the strength of LD between ith and jth markers, the spine of strong LD stretches along the edge of the triangular block pattern.
There have been several attempts to accelerates the speed and improve memory performance of the CI method in Haploview. Such attempts include MIG++ [12] and S-MIG++ [13] both of which can reduce the time/memory complexity by omitting unnecessary computations.
The MIG++ saves runtime and memory by omitting the computations of regions which have shown insufficient cases of strong LD. In addition, to improve the runtime/memory of the algorithm, the MIG++ uses a method based on an approximated estimator of the variance of DŌĆ▓ proposed by Zapata et al. [18] instead of the likelihood-based method proposed by Wall and Pritchard [19] used in Haploview [10]. The MIG++ algorithm is now implemented in PLINK 1.9 [14], but in PLINK 1.9, the CI of DŌĆ▓ is estimated based on the maximum likelihood method by Wall and Pritchard [19] with improved efficiency in estimating diplotype frequencies [13,20,21]. In this study, we only obtain the haplotype block partition results of the PLINK-MIG++ implemented in PLINK 1.9 instead of the originally proposed version of MIG++.
The S-MIG++ algorithm improves the MIG++ by first sampling small fraction of all SNP pairs to estimate the upper limits of the LD block boundaries and then moving to the refinement step to determine exact haplotype boundaries [13]. In this way, S-MIG++ could reduce the search space much more than MIG++.
The experiments have been conducted using the 1000 Genomes phase1 release 3 (1000G) data of East Asian populations (286 individuals from Japanese [JPT], Han Chinese from Beijing [CHB], and Han Chinese form South China [CHS]) [15] and HapMap phase III (HapMap) dataset of 170 individuals from JPT and CHB populations [16].
We used phased genotype data of 75,582 SNPs with minor allele frequency of 0.05 and without indel polymorphisms in chromosome 22 (chr22: 16,050,612ŌĆō51,243,297) in 1000G dataset, and the phased genotype data of 13,994 SNPs in chromosome 22 (chr22: 16,180,203ŌĆō51,219,006) in HapMap dataset after applying the same pruning criteria as the case of 1000G.
To construct experimental subsets of 1000G dataset with different density settings, we randomly selected 80%, 60%, 40%, and 20% of SNPs (resulting in 60,446, 45,349, 30,233, and 15,116 SNPs, respectively) of all SNP markers in the 1000G dataset in successive order by limiting the selection of SNPs within the SNPs already selected by the bigger subsets.
We applied the three Haploview methods (CI, FGT, and SS), PLINK-MIG++, and S-MIG++ to the entire 1000G dataset of chromosome 22, the entire HapMap dataset of chromosome 22, and the four datasets constructed from the 1000G dataset with the subsets of SNP markers chosen by the above method (80%, 60%, 40%, and 20% sampling ratio). To obtain results of CI, FGT, and SS, we constructed the moving windows of 1,000 SNPs for every 500 SNPs and run the Haploview program for each window region. When some block boundaries do not agree in the results of overlapped regions in consecutive windows, which occurs usually for the blocks at the boundary of a window, we construct a combined block region of two different block identification results and take it as the final haplotype block.
For PLINK-MIG++ and S-MIG++, there was no need to split the markers of the data used in our experiments due to enough capacity for runtime/memory of two programs. Note that in Haploview program, the CI method declares the size-2 blocks and size-3 blocks as haplotype blocks only when they do not span more than 20 kb and 30 kb, respectively. When we obtained the results using PLINKMIG++ and S-MIG++, we did not apply these limits for size-2 and size-3 blocks as the program does not allow this option. For the CI method, we set the option of Haploview to only consider the SNP pairs that are apart less than 500 kb such that the haplotype block size would be less than the limit. We applied the same condition about the distance between two SNPs in a pair to PLINK-MIG++, but not to S-MIG++ as the program does not allow this option. When we applied S-MIG++ program [13] to the experiments, we set the sampling fraction option of the first step of the algorithm to be 0.01.
In Table 1 and Fig. 1, a summary and trend of several characteristics of the haplotype block partition results are presented for five methods applied to each experiment data of 1000G and HapMap datasets. For each method with a sampling ratio setting, we calculated the total number of blocks, the average r2 values for all pairs of SNPs within a block and the average r2 values for pairs of which each SNP belongs to consecutive blocks, and the average size of haplotype blocks in terms of the number of SNPs in a block and the base-pair (bp) length of haplotype blocks. When we compared the haplotype block partition results based on 20% of original SNP markers to the results based on all SNPs in the 1000G dataset, the total number of haplotype blocks was reduced to about 40% in the CI, PLINK-MIG++, and S-MIG++ results and to about 30% in the FGT and SS results. Excluding the singleton blocks from the comparison, the amount of reduction was about 40% for all methods. For CI, PLINK-MIG++ and S-MIG++, the average length of the haplotype blocks based on 20% of original SNP markers in 1000G dataset was about 1.8 times of the length of the blocks produced using all SNPs for CI, PLINK-MIG++ and S-MIG++ and about 2.4 times for FGT and SS. With changes of sampling ratio of SNP markers, the average r2 within a same block remained almost unchanged, but the average r2 across consecutive blocks increased with the sampling ratio. The average r2 of S-MIG++ within a block and across consecutive blocks are slightly lower and higher than that of CI and PLINK-MIG++ and the difference in the haplotype block sizes is greater than the two methods even though S-MIG++ uses the same operational definition for LD block, which shows the fractional sampling methods adopted by S-MIG++ for computational efficiency also affects the LD block construction results.
Fig. 2 shows the LD heatmaps of an example region with the markers of haplotype blocks obtained by each method for five 1000G datasets of different sampling ratios and the HapMap dataset. We could observe that the big haplotype block regions that maintain strong LD in substantial proportion of SNP pairs are partitioned into several small blocks when using the entire SNP markers of 1000G dataset due to some breaks in the LD streaks, but with low sampling ratio subsets, many of these breaks disappear resulting in bigger sized haplotype blocks produced. The number of haplotype blocks obtained using the HapMap data was similar to the number of haplotype blocks obtained using 20% of SNPs of the original marker sets of 1000G dataset. However, actual locations of haplotype blocks obtained from two datasets were a little different.
In Fig. 3, we plotted the distributions of the length of the haplotype blocks produced from the 1000G datasets with different density levels and the HapMap dataset, for each method. The distribution of the length of haplotype blocks obtained from the HapMap dataset was similar to the one obtained from the 1000G dataset with 20% of the original markers. The frequencies of the haplotype blocks with length less than 30 kb decreases with the reducing density levels, but these frequencies were rather similar for big haplotype blocks in the results by all methods.
In Fig. 4, we present the proportions of commonly found haplotype blocks for each experimental dataset compared to the 1000G dataset with all SNP markers for each method. Only 7%ŌĆō10% of the haplotype blocks that are obtained using the entire SNP markers in the 1000G dataset are also observed in the result using 20% of the original SNP markers for CI, PLINK-MIG++, and S-MIG++ based on the 80% overlap criterion for common observation considering all blocks or excluding singleton blocks in the comparison. These proportions are even smaller for FGT and SS, only 3%ŌĆō 6% of haplotype blocks constructed from the entire markers are found when using 20% of original markers. When we compared only the haplotype blocks with sizes greater than 5,000 bp or 10,000 bp, the proportions of commonly found haplotype blocks from the datasets of all SNPs and 20% of SNPs increase to 21%ŌĆō28% for CI, PLINK-MIG++, and S-MIG++ whereas these proportions increase only to 8%ŌĆō 15% for FGT and SS. The effect of the density on the discovery of common haplotype blocks with results of full marker set was more severe in the results of FGT and SS compared to the other methods.
In this study, we investigated the effect of SNP marker density on haplotype block partition by comparing the haplotype block partition results based on subsets of the entire SNPs in the region. We observed that using only 20% of the original markers, the number of blocks produced by these methods reduces to 30%ŌĆō40% and the average length of the blocks increases to 1.8ŌĆō2.4 times of the results obtained using all SNPs. The effect of the density on the discovery of common haplotype blocks using a subset of the original marker set was almost linear for CI, PLINK-MIG++, and S-MIG++, and even exponential for FGT and SS methods as the density increases.
We could observe that the three haplotype block partition methods (CI, PLINK-MIG++, and S-MIG++) based on the definition of haplotype block by Gabriel et al. [8] tend to preserve more common blocks compared to the other two methods (FGT and SS) with low density marker sets. However, even for CI, PLINK-MIG++, and S-MIG++, the proportions of common blocks preserved with low density marker set decrease to below about 20% using 40% of the original markers when we decide 80% overlap as the common blocks considering only non-singleton blocks. Also, with low density marker sets of 20% or 40% SNPs, more than 75% or 65% haplotype blocks constructed from these low density sets were not found by the results using the entire SNP markers. In summary, the results using the entire SNP marker sets and results using less than half of the marker sets of the same dataset were quite different in all methods investigated in this study.
The FGT methods usually produces smaller size haplotype blocks than the other methods, and the SS methods produces bigger size haplotype blocks than the rest of the methods. However, both methods show low rates of finding common haplotype blocks from the dataset with different density levels compared to CI, PLINK-MIG++, and S-MIG++. Both methods define a haplotype block if strong LD is maintained for all SNPs with each other (FGT) or with the first and last SNPs (SS). From the 1000G dataset with the full set of all SNPs, we could observe that some extensive LD regions where the strong LD is shown between some non-consecutive markers which cannot be considered as in the same block region by FGT or SS by their definition the haplotype block. Consequently, these LD regions are split into small regions when using high density SNP markers, but with low density markers, there are more chance to find bigger haplotype block. The most of haplotype block partition methods have been developed using relatively low density such as the HapMap data rather than the whole genome sequencing data such as the 1000 Genomes Project [10]. The recent methods such as PLINK-MIG++ and S-MIG++ is mere computational improvement of the CI method resulting in similar block partition results as the Haploview-CI algorithm. This study shows that researchers should be very careful when they use the haplotype block construction results from reference panel data for the analysis and interpret genetic analysis using different genotype data with different marker density. Also, there is need for a new method that finds more marker-independent haplotype blocks regardless of the selection of the SNP markers, especially the one that works well for high density SNP markers such as 1000 Genomes Project dataset.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) grant NRF-2015R1A1A3A04001269 and NRF-2015R1A2A2A01006885.
References
1. Slatkin M. Linkage disequilibrium: understanding the evolutionary past and mapping the medical future. Nat Rev Genet 2008;9:477ŌĆō485. PMID: 18427557.



2. Reich DE, Cargill M, Bolk S, Ireland J, Sabeti PC, Richter DJ, et al. Linkage disequilibrium in the human genome. Nature 2001;411:199ŌĆō204. PMID: 11346797.


3. Daly MJ, Rioux JD, Schaffner SF, Hudson TJ, Lander ES. High-resolution haplotype structure in the human genome. Nat Genet 2001;29:229ŌĆō232. PMID: 11586305.


4. Sabeti PC, Varilly P, Fry B, Lohmueller J, Hostetter E, Cotsapas C, et al. Genome-wide detection and characterization of positive selection in human populations. Nature 2007;449:913ŌĆō918. PMID: 17943131.



5. Greenspan G, Geiger D. Model-based inference of haplotype block variation. J Comput Biol 2004;11:493ŌĆō504. PMID: 15285904.


6. Jeffreys AJ, Kauppi L, Neumann R. Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat Genet 2001;29:217ŌĆō222. PMID: 11586303.


7. Twells RC, Mein CA, Phillips MS, Hess JF, Veijola R, Gilbey M, et al. Haplotype structure, LD blocks, and uneven recombination within the LRP5 gene. Genome Res 2003;13:845ŌĆō855. PMID: 12727905.



8. Gabriel SB, Schaffner SF, Nguyen H, Moore JM, Roy J, Blumenstiel B, et al. The structure of haplotype blocks in the human genome. Science 2002;296:2225ŌĆō2229. PMID: 12029063.


9. Wang N, Akey JM, Zhang K, Chakraborty R, Jin L. Distribution of recombination crossovers and the origin of haplotype blocks: the interplay of population history, recombination, and mutation. Am J Hum Genet 2002;71:1227ŌĆō1234. PMID: 12384857.



10. Barrett JC, Fry B, Maller J, Daly MJ. Haploview: analysis and visualization of LD and haplotype maps. Bioinformatics 2005;21:263ŌĆō265. PMID: 15297300.


11. Ardlie KG, Kruglyak L, Seielstad M. Patterns of linkage disequilibrium in the human genome. Nat Rev Genet 2002;3:299ŌĆō309. PMID: 11967554.


12. Taliun D, Gamper J, Pattaro C. Efficient haplotype block recognition of very long and dense genetic sequences. BMC Bioinformatics 2014;15:10. PMID: 24423111.



13. Taliun D, Gamper J, Leser U, Pattaro C. Fast sampling-based whole-genome haplotype block recognition. IEEE/ACM Trans Comput Biol Bioinform 2016;13:315ŌĆō325. PMID: 27045830.


14. Chang CC, Chow CC, Tellier LC, Vattikuti S, Purcell SM, Lee JJ. Second-generation PLINK: rising to the challenge of larger and richer datasets. Gigascience 2015;4:7. PMID: 25722852.




15. 1000 Genomes Project Consortium. Abecasis GR, Auton A, Brooks LD, DePristo MA, Durbin RM, et al. An integrated map of genetic variation from 1,092 human genomes. Nature 2012;491:56ŌĆō65. PMID: 23128226.



16. International HapMap 3 Consortium. Altshuler DM, Gibbs RA, Peltonen L, Altshuler DM, Gibbs RA, et al. Integrating common and rare genetic variation in diverse human populations. Nature 2010;467:52ŌĆō58. PMID: 20811451.



17. Lewontin RC. The interaction of selection and linkage. I. General considerations: heterotic models. Genetics 1964;49:49ŌĆō67. PMID: 17248194.




18. Zapata C, Alvarez G, Carollo C. Approximate variance of the standardized measure of gametic disequilibrium D'. Am J Hum Genet 1997;61:771ŌĆō774. PMID: 9326344.



19. Wall JD, Pritchard JK. Assessing the performance of the haplotype block model of linkage disequilibrium. Am J Hum Genet 2003;73:502ŌĆō515. PMID: 12916017.



20. Hill WG. Estimation of linkage disequilibrium in randomly mating populations. Heredity (Edinb) 1974;33:229ŌĆō239. PMID: 4531429.


21. Gaunt TR, Rodr├Łguez S, Day IN. Cubic exact solutions for the estimation of pairwise haplotype frequencies: implications for linkage disequilibrium analyses and a web tool 'CubeX'. BMC Bioinformatics 2007;8:428. PMID: 17980034.



Fig.┬Ā1
The effect of sampling ratio of the experimental datasets sampled from the 1000G dataset and HapMap dataset on several summary statistics of haplotype blocks obtained by five haplotype block partition methods. SNP, single nucleotide polymorphism; CI, confidence interval; FGT, four gamete test; SS, solid spine.
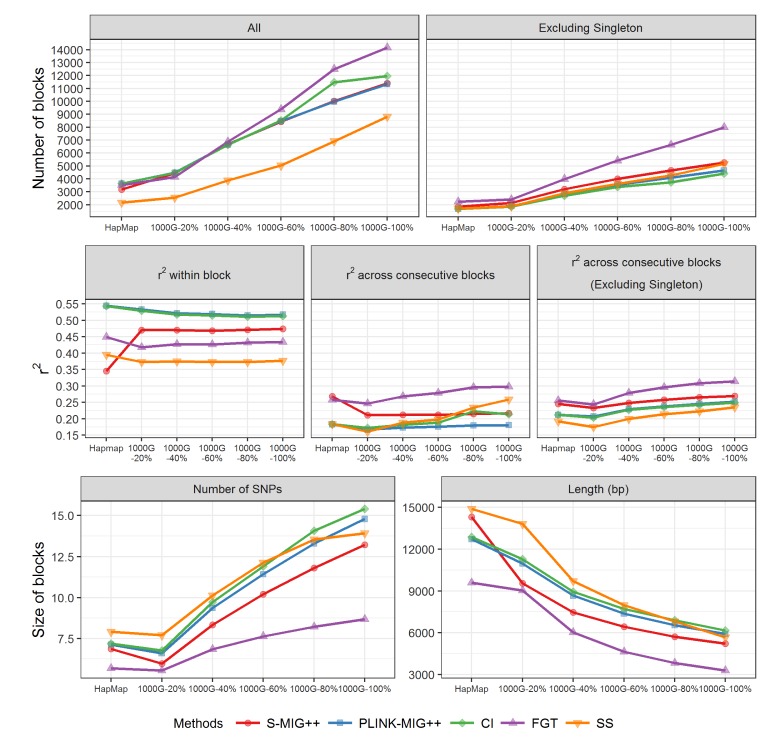
Fig.┬Ā2
(AŌĆōF) LD heatmaps and haplotype block partition results of an example region of chromosome 22: 37,908,435ŌĆō 37,972,438 bp. Only non-singleton blocks found by each method are marked in orange colored rectangles. Two blue colored arrows in each of LD heatmaps are pointing the locations of 37,935,945 bp and 37,960,051 bp. LD, linkage disequilibrium; CI, confidence interval; FGT, four gamete test; SS, solid spine.
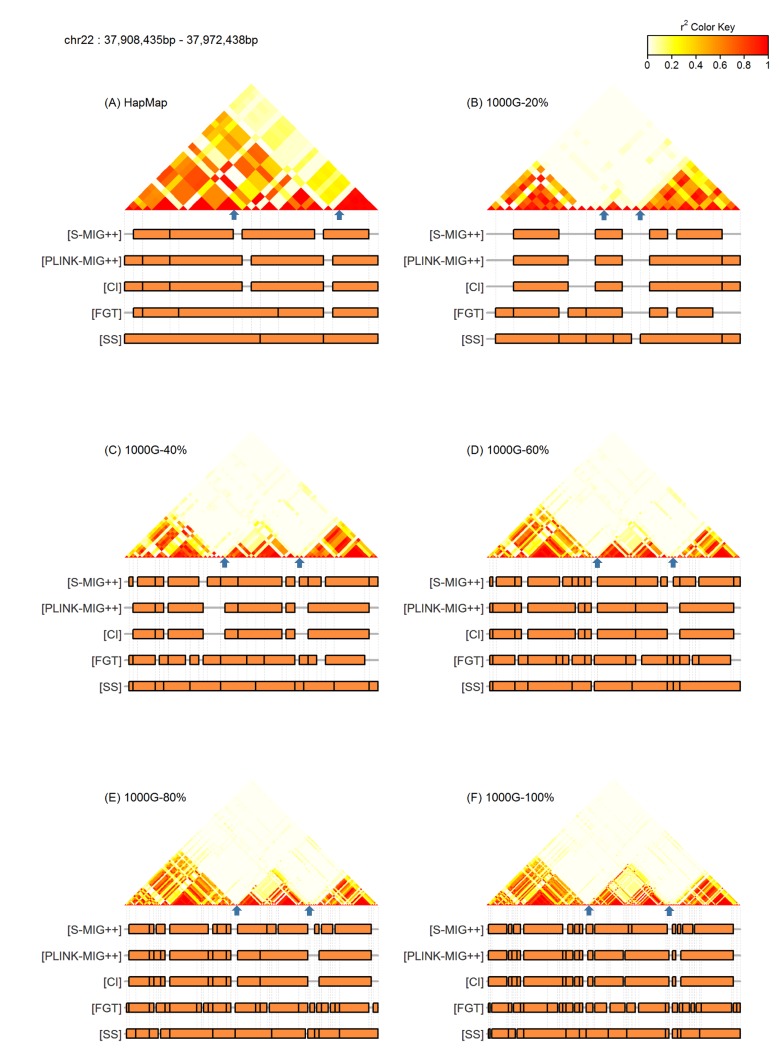
Fig.┬Ā3
Distributions of the length of haplotype block found by S-MIG++, PLINK-MIG++, CI, FGT, and SS obtained using chromosome 22 region of the HapMap dataset and the 1000G dataset with different sampling ratios. CI, confidence interval; FGT, four gamete test; SS, solid spine.
Fig.┬Ā4
The proportion of commonly found haplotype blocks based on the marker subset of 1000G dataset and the HapMap dataset compared to the entire 1000G SNP markers. Two haplotype blocks obtained from each of two datasets are said to be common blocks if Lo/Lw or Lo/Ls is greater than or equal to 0.8 where Lo is the length of overlapped region of a pair of haplotype blocks, Lw is the length of a block in entire data which overlapping with the block in sampled data, and Ls is the length of a block in sampled data which overlapping with the block in entire data. SNP, single nucleotide polymorphism; CI, confidence interval; FGT, four gamete test; SS, solid spine.

Table┬Ā1.
A summary of haplotype block partition results obtained for chromosome 22 region of experiment datasets of various sampling ratio sampled from the 1000G dataset and the HapMap dataset
- TOOLS
-
METRICS

-
- 7 Crossref
- 0 Scopus
- 6,689 View
- 104 Download





